Presión sonora y sonoridad
Presión sonora y sonoridad (I): percepción del nivel audio
A veces pensamos en la sonoridad un tanto ciegamente, aplicando sin mucha reflexión los dBSPL. Con una cadena de tutoriales buscamos entender y no sólo operar con la sonoridad, como continuación de nuestras entregas sobre acústica y electrónica.
Presión sonora: significado, unidades y umbrales de audición
El sonido corresponde a las variaciones de presión en el aire, mediante compresiones y rarefacciones en torno a la presión atmosférica. A la postre no necesitamos saber mucho de presión y sus unidades, porque nos hemos inventado algo (el nivel de presión sonora y los dBSPL) para tener una escala útil y sencilla de entender y aplicar. Pero eso no impide que nos interesemos por observar algunas características curiosas que asoman cuando pensamos en términos de presión y sus unidades.
La presión usa como unidad el Pascal (Pa). Por ejemplo, la presión atmosférica ronda aproximadamente los 100.000 Pa, en función de las condiciones climáticas, la altura sobre el nivel del mar, y otras condiciones.
Respecto a ese valor las variaciones que causan los sonidos son realmente pequeñas. La variación de presión en los picos de aquellos sonidos que ya comienzan a infligir dolor es de tan solo 20 Pa, mientras que los sonidos apenas perceptibles desarrollan una excursión de sólo 0,00002 Pa, también escrita como 20 x 10-6 Pa, valor de presión conocido como umbral auditivo.
Siendo como es irrelevante la presencia permanente de 100000 Pa ’atmosféricos’ e interesándonos sólo por las variaciones en torno a ese valor, se ha definido la presión sonora como aquella que resulta de retirar en la medida la aportación de la presión atmosférica, haciendo que el rango de esta así llamada presión sonora se extienda de 0,00002 a 20 Pa, o lo que es lo mismo de 20 x 10-6 Pa hasta 20 Pa. No es nada despreciable la extensión que supone, con el mínimo de presión sonora detectable un millón de veces por debajo de aquel valor que produciría dolor (y que por tanto es a efectos prácticos una cota máxima que no conviene rebasar). El uso del micro Pascal o μPa, permite reexpresar el umbral auditivo como 20μPa con mayor comodidad.
| Presión sonora | |
| Umbral de audición | 20 μPa |
| Umbral de dolor | 20 Pa |
Se trata de valores medios usados como referencia, con diferencias para cada persona y también en función del tipo de sonido, su forma de onda y su frecuencia.
Existen sistemas de reproducción audio que van mas allá del nivel de dolor, pero lo normal será que no se usen tan cerca de los oyentes como para que les llegue esa gran presión. Así no es extraño que en la inmediata proximidad a un altavoz o un cluster las presión pueda ser incluso peligrosa/dañina. Pero estarán tan alejados de la audiencia que lo que llegue a esta será un nivel más tolerable. No debe extrañarnos por tanto que muchos sistemas de reproducción especifiquen que son capaces de generar niveles de presión sonora a un metro (que es la distancia a la que muchas veces se dan estas características en las especificaciones) muy por encima no ya de umbrales de dolor sino incluso llegando a valores capaces de provocar daño instantáneo en el tímpano.
Sonoridad vinculada a ¿amplitud o energía?
Lo de los pascales y la presión sonora nos habla de cómo medir una característica física, pero no nos dice cómo sentimos/percibimos el nivel en las señales audio.
Es interesante destacar desde un primer momento que, cara a la percepción de un sonido como fuerte o débil, nuestra audición reacciona más bien al cuadrado de la presión. Para que notemos la sensación de oír un sonido de doble fuerza (una apreciación subjetiva, que se ha caracterizado estadísticamente con pruebas y tests con personas) basta que el cuadrado de la presión se haya doblado, no hace falta que la amplitud de la presión se doble, no necesitamos llegar a doblar la presión.
Hemos prometido no ser muy ‘científicos’ ni exigentes en lo teórico-matemático, así que demos por bueno que esa percepción ligada al cuadrado del valor de la amplitud habla de que nuestro oído siente la ‘energía’ y no la ‘amplitud’. [En física la energía y la potencia son magnitudes guardan siempre una relación cuadrática con la amplitud del campo -en nuestro caso con la presión sonora-, así que a veces veréis hablar de energía o potencia de forma semejante: aunque son cosas distintas, son parientes cercanas. Al final tenéis un complemento sobre esta cuestión].
Lo que quiero destacar es que no sentimos la amplitud que vemos en el osciloscopio ni la que representa la gráfica de la señal en un DAW. Si bajamos a la mitad esa amplitud no oímos la mitad de fuerte, la oímos unas 4 veces más débil (2 al cuadrado).
Hablamos de sonoridad para indicar esa ‘sensación’ de la fuerza o intensidad sonora tal como la percibimos los humanos, y que globalmente vinculamos con la energía, no con la amplitud de la señal sonora (digo ‘globalmente’ porque hay también diferencias en cómo de fuertes oímos los sonidos en distintos rangos de frecuencias y otras cuestiones que presentaremos otro día).
Por tanto, partiendo de un sonido de presión sonora X (Pa), conseguir una sensación de sonido cien veces más intenso (en energía) exigiría sólo diez veces esa presión (amplitud) de partida, es decir 10X (Pa), no 100X (Pa). De forma semejante conseguir la sensación de sonido doblemente intenso (una sonoridad doble) requeriría una presión sonora de 1.41X (Pa), porque la raíz de dos es 1,4142…
Desde esa perspectiva, el recorrido ya de por sí amplio de un millón de veces que separa la mínima y la máxima presión sonora (los 20micropascales y los 20 pascales), se convierte al elevar al cuadrado los extremos para obtener los correspondientes valores de potencia en nada menos que un millón de millones de veces más potencia. Esa es la apabullante diferencia de sensaciones que podemos llegar a encontrar en nuestra percepción de los sonidos. Un recorrido que, por ser tan extenso, se vuelve difícil de manejar numéricamente, por lo que se han concebido otras representaciones más compactas, en concreto se aplican medidas en dB (decibelios). [Sobre los dB hemos presentado ya varios tutoriales que recordaremos un poco más adelante.]
La sensación de sonoridad no es instantánea, sino ‘promedio’
Otra cuestión que hemos de recalcar en cuanto a la percepción de la sonoridad: está vinculada al comportamiento global de la señal, no a su detalle. Son los sonidos señales oscilantes, como por ejemplo lo es una sinusoidal. Pero no tenemos sensación de que su sonoridad varíe durante las evoluciones de cada ciclo, sino sólo de forma más agregada, sólo sensible al promedio. Nuestra escucha de las variaciones microscópicas / de detalle se expresa en las sensaciones de timbre, no en las sensaciones de nivel. Nuestra escucha del nivel es siempre macroscópica por comparación. Algo que nos lleva de forma natural a presentar el concepto de envolvente, y también a precisar qué significa una medida RMS o Root Mean Square, unas siglas frecuentes en audio.
El concepto de ‘envolvente’
Una representación cuya escala temporal sea de muy pocos milisegundos o pocas decenas de milisegundos nos permite ver el detalle exhaustivo de la señal, cada una de sus subidas y bajadas de nivel/presión. Pero cuando representamos la señal a otras escalas más amplias (cuando hacemos un ‘zoom out’) este detalle necesariamente se pierde, y lo habitual es que se represente algún tipo de (así llamada) ‘envolvente’: una traza del contorno general, pero ya sin el detalle al completo. Perdemos la visión de los ciclos individuales de subida/bajada de la presión y nos quedamos sólo con una referencia global o promedio de nivel.
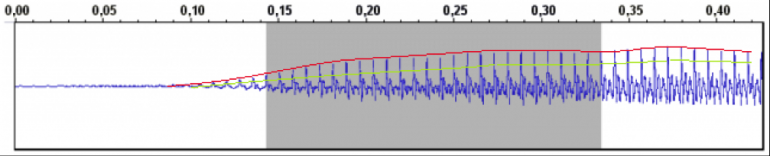
Algo semejante sucede con nuestra sensación de la fuerza o nivel de los sonidos. Sólo la sentimos, como decíamos, en una especie de promedio, de tendencia. Dicho nivel promedio puede verse como la línea roja creciente en esta gráfica (que esencialmente representa un contorno elaborado a partir de los picos de la señal) o como la línea verde (que traza una especie de nivel promedio). Son sólo dos ejemplos de cómo podríamos intentar concebir y representar una idea del comportamiento global de nivel.
Esa figura anterior ya manifiesta la posibilidad de diferentes formas de considerar la evolución ‘global’. Mientras que la señal instantánea y detallada está definida de forma única, a la hora de caracterizar su envolvente podemos decantarnos por diferentes representaciones. Tanto la línea roja como la verde nos informan de una señal que manifiesta un nivel creciente a lo largo del tiempo y que finalmente parece estabilizarse. Pero son dos contornos distintos.
En la construcción de esos contornos o envolventes de una señal intervienen dos pasos: una rectificación primero y algún tipo de promediado después.
La rectificación: el nivel no es bipolar
El nivel que sentimos sólo distingue en un recorrido absoluto fuerte/débil, no hay una sensación de nivel 'negativo'. Pese a que la señal original es bipolar, no tenemos sensación de oír dos niveles diferentes sino sólo uno. Aunque la señal sea tan asimétrica como la que muestra la anterior imagen, oímos 'un' nivel.
Dicho desde una perspectiva más formal, sabiendo que escuchamos en función de la energía, el signo de la señal nos da igual: la energía usa una versión cuadrática de la amplitud y por tanto siempre positiva. Como consecuencia una cuestión que asoma en todas estas representaciones ‘de envolvente’ es la irrelevancia de mantener el carácter bipolar que originalmente tiene la señal.
Esto lleva a considerar la llamada ‘rectificación’ de la señal como primer paso en la obtención de la envolvente. Hay dos formas de rectificación: de media onda y de onda completa.
- Rectificación de media onda implica anular la señal por debajo del nivel cero y quedarnos sólo con la parte positiva. Era un cambio muy sencillo desde el punto de vista de la electrónica, y generalmente el impacto que causa sobre la estimación del nivel no es grave. Pero incluso el estándar para los VU meter hablaba de rectificar en onda completa, no en media onda.
- Rectificación de onda completa implica invertir la señal negativa para que tome valores positivos. Es equivalente a quedarnos con el ‘valor absoluto’ de la señal.
Pero además de la cuestión de la rectificación (en la que los sistemas suelen decantarse por la de onda completa, salvo que intervengan razones de coste), está la otra no menos importante.
El promediado y la duración del ‘ventana de observación’
Cualquier envolvente implica eliminar detalle y quedarnos sólo con la tendencia. Eso exige tomar alguna decisión sobre la duración del intervalo durante el cual vamos a ‘integrar’ el comportamiento de la señal y esquivar su estructura interna reemplazándola por un valor conjunto. Cuál es la duración o ventana del promediado, el ‘tiempo de reacción’ con el que se producen las evoluciones de la envolvente, importa e impacta mucho en el resultado.
En nuestro caso, con ciclos que llegan a los 50ms en el registro grave, no son extraños tiempos de reacción de pocos cientos de ms. Es el caso por ejemplo de la aguja de los vúmetros, cuya inercia responde aproximadamente con tiempos del orden de unos 300ms.
Tendremos ocasión de hablar en profundidad sobre el efecto de las constantes de tiempo cuando presentemos los compresores y otros sistemas de alteración de la dinámica, en los que el usuario suele poder ajustar los tiempos de ataque y de relajación, a través de los cuales se pueden conseguir resultados muy diferentes. Por ello no ahondaremos ahora mismo en esta cuestión más allá de citar su importancia. De hecho no sólo la duración, también la 'forma' de la ventana impacta, pero por hoy nos basta reconocer que diferentes duraciones provocarán diferentes envolventes, unas más marcadamente globales y lentas, otras capaces de hacer un seguimiento algo más fino y ágil ante los cambios.
Resumiendo
- La presión sonora es una medida de amplitud de la señal sonora, en la que no consideramos la presencia de la presión atmosférica sino las excursiones en torno a ella.
- Los umbrales de la audición humana son tales que permiten detectar sonidos con valores de presión sonora desde los 0,00002 hasta los 20 Pascales, un amplio recorrido en el que el mínimo es 1 millón de veces menor que el máximo.
- Pasando a la cuestión de cómo sentimos, la sonoridad la percibimos en función de la energía (no de la amplitud) y siempre de forma agregada/promediada en un amplio tiempo.
- La obtención de la envolvente de una señal implica rectificar y promediar, y admite múltiples maneras de resolver la cuestión.
Como supongo que os habrá sabido a poco la entrega de hoy, no vamos a demorar la aparición de la siguiente, centrada en presentar qué son el valor RMS y el vúmetro. Pero me parecía adecuado asegurar una mirada común sobre estas cuestiones de hoy que impregnarán esa siguiente entrega.
Además para no dejar tan corto de contenidos este tutorial, aprovecho para colaros algo que podéis tomar como opcional. Dado que hemos hablado de que sentimos el nivel audio vinculado a la energía, quería comentar la diferencia energía/potencia. No lo veo esencial para manejarnos en la vida diaria, y de hecho según los países y los libros veréis usar uno u otro término (especialmente en casos como 'energía media' que para algunos es una aberración porque prefieren llamarlo potencia, por ejemplo).
Una aclaración: energía vs potencia
Como siempre en esta serie intentaremos no ser muy matemáticos/físicos, pero sí conviene una mención al menos a los parecidos y diferencias entre energía y potencia. A veces los usamos de forma casi indistinta en la vida ordinaria, para horror de los físicos. Y es que energía y potencia no son lo mismo, pero siempre resultan en física de una relación cuadrática con la amplitud, que es el hecho que para nosotros nos interesa destacar y que a veces nos lleva a confundir o usar indistintamente ambos términos.
En ese sentido, si llamamos s(t) a una señal que representa la amplitud o nivel instantáneo de nuestra señal, podríamos pensar en una nueva señal que represente la ‘energía instantánea’ o la ‘potencia’ de esa señal y que sería [s(t)]2 también escrita a veces como s2(t).
Por ejemplo, en electrónica la potencia (P, vatios) es el producto de la tensión (V, voltios) y la corriente (I, amperios), es decir P= V I. Pero como la ley de Ohm establece entre V e I una relación a través de la resistencia (R, ohmios) descrita como V = I R, podemos llegar a que P = V I = R I2 = V2 / R, expresiones que hacen patente esa relación cuadrática, más allá de la compañía de un factor R multiplicando o dividiendo. Ese producto P = I R era la potencia. Para poder valorar energía necesitamos además introducir el tiempo, pero seguirá tratándose de una relación cuadrática con la amplitud (ya sea medida en tensión –voltios- o en intensidad –amperios-).
Sobre la diferencia entre energía y potencia es bastante evidente este ejemplo: Los 100W indicados en una bombilla hablan de su consumo instantáneo cuando esté alimentada en las condiciones normales de la red de suministro eléctrico (los 220V AC en España). Es la potencia que gasta en condiciones normales de trabajo, la potencia que exige le sea entregada en todo momento para producir luz adecuada. La energía que consume esa bombilla al usarla es el producto de esa potencia que gasta al producir luz por el tiempo durante el que la tengamos encendida.
Lo que quiero destacar es que la medida de energía siempre está referida al total de un tiempo de observación, mientras que la potencia no hay esa presencia del factor tiempo. Una bombilla de 100W de potencia que esté encendida 10 horas al día consumirá 100x10 = 1000Wh de energía cada día, es decir, 1kWh por día (que viene a costar unos 15 o 20 céntimos de euro a precio actual en España). Esa es la energía diaria que consumiríamos.
Otro ejemplo también muy claro es el de la factura de la luz y sus términos fijo y variable: el término fijo es por potencia contratada (cuántos kW queremos garantizar que se nos puedan llegar a servir desde la red) y el término variable es por energía consumida (nos cobran por los kWh que hemos usado realmente: un resultado de integrar a lo largo del tiempo la demanda de energía que efectivamente hemos absorbido de la red). En la energía aparece esa idea de un determinado tiempo de observación: cuánta potencia hemos absorbido de la red durante cierto tiempo. Los 3300W de potencia contratada que muchos tenemos en nuestro contrato de suministro para el hogar hablan del máximo de potencia que vamos a pedir a la suministradora. No indica ningún consumo real, sólo la capacidad de llegar a desarrollar un cierto trabajo o esfuerzo (en este caso llegar a alimentar equipos eléctricos que agregadamente no exijan rebasar ese límite). La mayor parte del tiempo consumimos menos. Sólo si nos pasamos ‘saltan los plomos’ o ‘se va la luz’, como suele decirse.
En consonancia con lo dicho, la potencia tiene unidades de W, mientras la energía aplica unidades basadas en un producto potencia y tiempo, como esos kWh (producto de kilovatios y hora).
Parecería más correcto, desde la perspectiva de las unidades, hablar de potencia (y no de energía instantánea, aunque a veces se vea así dicho) cuando se trata de un valor instantáneo y por tanto sin referencia a una duración o plazo. También sería potencia (W) lo que usaríamos para hablar de un valor pico en el que tampoco interviene el tiempo (como podría ser aquella potencia que puede llegar a estropear un equipo, que sería su potencia máxima admisible –no decimos energía instantánea máxima antes de romperse-).
También oímos hablar de potencia media (y no de energía media consumida) cuando calculamos un promedio de la energía a lo largo de un tiempo, cosa que ilustra este ejemplo: Después de estar encendida 10 horas esa bombilla de la que hablábamos el contador ha subido 1kWh (ha gastado un kWh de energía), lo que indica un consumo medio de 0.1kW, o sea 100W. Un valor que aunque ha sido calculado mediante un promedio temporal de la energía algunos no llaman energía media, sino que prefieren toldar de potencia por aquello de que sería raro llamar energía (aunque fuera media) a algo que tiene unidades de W.
Presión sonora y sonoridad (II): valor RMS, vúmetros y picómetros
Introducción: los viejos medidores nunca mueren
Recuerda que este tutorial es continuación de una entrega anterior. En ella hablábamos de cómo sentimos el nivel de las señales audio. Lo sentimos no por la amplitud (presión sonora) sino por la energía (vinculada al cuadrado de la amplitud), y de forma ‘promediada’ no instantánea. A este respecto es habitual caracterizar en las señales su valor RMS y aplicar una representación dinámica del nivel de la señal a lo largo del tiempo a través de los llamados vúmetros. Ambos dan entrada en mediciones objetivas a algunas características propias de nuestra percepción subjetiva del nivel de las señales audio. Por otra parte diferentes tipos de picómetro se usan para poder valorar el mayor nivel que presenta una señal, que tiene interés sobre todo cara a no causar problemas (saturaciones, recortes) en los sistemas que atraviese esa señal.
Tanto los medidores RMS como lo vúmetros y muchos de los así llamados picómetros 'a la antigua usanza' deberían ir desapareciendo en favor de otras estrategias de medida que se han estandarizado después (como EBU R128) y que tienen mucha mayor capacidad de informar sobre las cuestiones que interesan que estas otras. Pero aunque las mediciones EBU R128 son no ya sólo recomendables sino cada vez más exigidas, lo son a efectos del producto final (p.ej. midiendo un máster estéreo). Allí donde se necesita visualizar muchas señales (cualquier mesa o sistema multipista) la exigente definición de EBU R128 resulta desproporcionada y se tiene por suficiente orientación la que dan vúmetros y picómetros más tradicionales, y también de mucho menor coste y complejidad.
Los medidores de tipo RMS, VU y PPM (Peak Program Meter) forman una vieja escuela que se resiste a desaparecer, y conocerlos y diferenciarlos sigue siendo necesario.
Tutoriales sobre los dB (decibelios)
Es apropiado revisar en este punto algunos otros tutoriales que ya hemos publicado en otros momentos y en los que encontraréis una presentación de los dBs:
Así mismo, para lo que vamos a contar hoy, es bueno que entiendas la diferencia en el uso de unidades de tipo dB para caracterizar potencia/energía y para caracterizar amplitud. Algo que intentábamos abordar en esta otra entrega.
Puedes optar por leer esos tutos antes de este o bien por volver a ellos si no te encuentras del todo cómodo con algo de lo que contamos hoy.
Valor RMS (root mean square), valor pico, valor pico-pico
A partir del discurso que hicimos en la entrega anterior, sabemos que sentimos la energía, no la amplitud, y que sentimos un 'promedio' de la energía, no sus variaciones instantáneas. No extrañará entonces que se prefiera abordar los cálculos de ese promedio sobre la energía incluso cuando los resultados a veces luego se ofrezcan en términos de amplitud. Esto es lo que sucede cuando hablamos del valor RMS de una señal.
Nuestras representaciones gráficas en un DAW, la representación de señal en un osciloscopio, los valores medidos por un polímetro… son todos valores referidos a la amplitud. Es la amplitud un ámbito habitual para la representación, aunque nuestra sensación auditiva venga vinculada a la energía. El cálculo del valor RMS permite obtener un valor `promedio’ de la energía de una señal cíclica pero describirlo a través de una ‘amplitud’ equivalente de forma que ese valor RMS (por las siglas en inglés de ‘root mean square’) pueda compararse con las representaciones y mediciones habituales, casi siempre realizadas en amplitud.
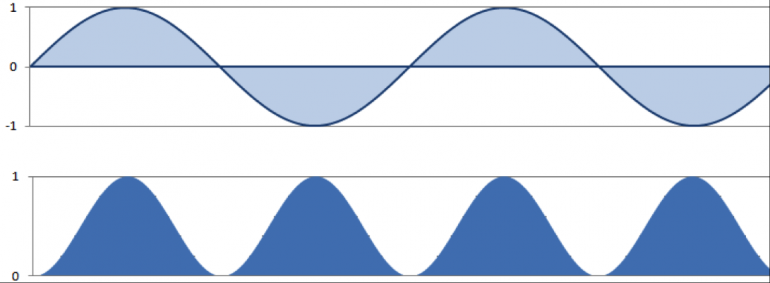
Pensemos en una señal cuya amplitud esté definida por s(t). Sin pérdida de generalidad, a efectos de ilustrarlo, haremos representación de una sinusoidal. Si pintamos también la senoide al cuadrado:
El seno al cuadrado (proporcional por tanto a la energía del seno original) resulta ser una nueva senoide de frecuencia doble que ahora oscila entre 0 y 1 (un resultado que no vamos a justificar aquí pero que es fácil de verificar con reglas básicas de trigonometría).
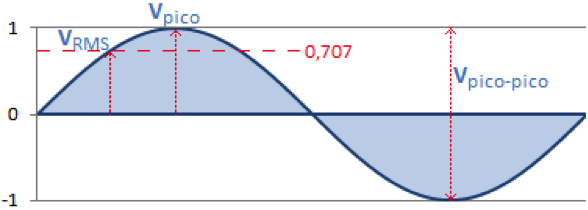
El valor medio de una señal audio s(t) es cero (son señales sin DC) y por tanto no nos dice nada de si era una señal grande o pequeña. Pero podemos calcular el valor medio de su cuadrado, que resulta ser 0,5 en el caso de la sinusoide anterior. Podemos concebir que el valor promedio del cuadrado de la señal caracteriza la energía en promedio de nuestra señal. Por ser un valor promedio en energía es además más significativo perceptualmente.
Por otra parte, ese mismo valor es la energía que tendría una señal de amplitud constante e igual a la raíz cuadrada de 0,5 lo que arroja el resultado 0,707. Nuestra senoide original, oscilante (AC) entre +1 y -1 desarrolla la misma energía que una señal constante (DC) de amplitud 0,707. Este tipo de cálculo es el que se denomina RMS, y habla del valor de amplitud de una señal de nivel constante (DC) que tendría la misma energía que la señal estudiada.
En el caso del seno, el valor RMS es de 0,707 veces el valor de pico.
Otras formas de señal pueden tener otros valores RMS. Si pensáis en una señal cuadrada, su valor pico y su valor RMS coinciden, podéis pensar vosotros mismos porqué.
Con señales cíclicas como las que venimos comentando el cálculo puede hacerse sobre un único periodo y valdrá para cualquier momento, pero con señales no cíclicas estaremos normalmente estimando un valor RMS extendiendo el promedio sobre cierta duración de observación. En esos casos no se tratará de un valor constante, sino variable. Evolucionará describiendo subidas y bajadas de nivel a modo de una envolvente, un contorno que permitirá seguir las variaciones de nivel RMS de la señal.
Aunque los vúmetros son lo primero que viene a la cabeza cuando pensamos en medidores, en algunos sistemas contamos también con medidores RMS. Los analógicos suelen ser aproximados, no exactos (el cálculo del valor RMS en analógico no es trivial).
En el caso de implementaciones digitales pueden ser medidores de verdadero valor RMS (calculan la media del cuadrado de la señal) con tiempo de promediado a veces fijo y en el orden de los 300ms. (por ser la constante de tiempo típica en vúmetros) y otras veces ajustable por el usuario.
El vúmetro
Vúmetros y picómetros son dos herramientas habituales en audio, con objetivos bien diferentes.
Un vúmetro (nombre coloquial -no existe en el diccionario RAE-) o ‘VU meter’ mide los llamados Volume Unit (VU) como forma de representar algo parecido al nivel percibido del audio. Existen normas internacionales que describen en detalle sus características y requisitos (ANSI C16.5-1942 y otras posteriores) pero que no necesitamos conocer en profundidad.
Si en RMS hablábamos de calcular el cuadrado (energía) para acabar obteniendo un valor de amplitud, en el caso del vúmetro se trata de un tipo de medidor (un galvanómetro de aguja, como el de los voltímetros) que mide la corriente (por tanto una amplitud). Pero el etiquetado del medidor usa una escala en decibelios, y por tanto se hace en términos de energía/potencia: las marcas, además del 0 VU que indica un punto de referencia, se realizan a +/-3 dB (potencia doble/mitad respecto al umbral) y semejantes. Como resultado la lectura sobre la escala de un vúmetro nos muestra un valor relacionado con la energía de la señal y sus variaciones a lo largo del tiempo, y lo hace aplicando una escala en dB y un promediado que resulta ser bastante largo.
Físicamente los vúmetros de aguja hacen pasar una corriente por la bobina acoplada a la aguja que proviene de rectificar (onda completa) la señal audio. La bobina, por estar dentro del campo magnético producido por un imán, se desplaza en función de esa corriente. Pero la inercia mecánica del conjunto más la electrónica que lo acompaña hacen que haya un tiempo de reacción que dista de ser instantáneo. El tiempo de integración del conjunto está en unos 300 ms (tanto de activación como de desactivación), con lo que cambios veloces (como los que se dan en muchísimos transitorios en audio) no llegan a visualizarse. A cambio sí se obtiene un desplazamiento que encaja aproximadamente con una cierta sensación de sonoridad basada en ese promedio.
Ya hemos mencionado que las marcas realizadas en la escala del galvanómetro vienen etiquetadas en dB, de forma que expresan energía/potencia aunque la aguja se mueve por acción de la corriente (amplitud). Como pasa a todos los sistemas basados en estos galvanómetros de aguja, los valores sólo son relativamente fiables en la zona de amplia deflexión (desplazamiento) de la aguja, mientras en las zonas de poco recorrido el grado de error posible sube. Pero como el interés de estos medidores está en poder vigilar los momentos fuertes, no es una pega seria. Existen también vúmetros realizados con barra de leds, en sustitución de la aguja, y un circuito que puede ser analógico o digital para definir el patrón de iluminación en cada momento.
Los VU meters ‘serios’ están además calibrados y rotulados de forma tal que se puede saber qué nivel de señal eléctrica promedio los atraviesa. En su escala en decibelios, el nivel 0 VU debería corresponder a una señal de nivel +4dBu, que es un valor estándar en interfaces audio del que hemos hecho presentación en otro tutorial acerca de los niveles estándar de línea +4dBu y -10dBV. Pese a todo, debería consultarse en el manual de cada equipo qué es lo que realmente indica la posición 0 VU, puesto que hay equipos que lo hacen corresponder a 0 dBu (y más raramente a otros valores) en lugar de a +4 dBu. En algunos casos veréis de hecho que no usan el nombre 'VU meter' sino 'dB meter' y siempre conviene conocer la correspondencia real.
De los valores medios a los cresta: la holgura de los sistemas
Recordad en todo caso que ese valor 0 VU y los +4dBu que suele representar, son un nivel estandarizado para facilitar la interconexión de sistemas audio profesional, pero que estos sistemas admiten señal por encima de ese nivel sin entrar todavía en niveles de distorsión severos. Cuando las señales se trabajan a nivel analógico, se sabe que los sistemas tendrán unos codos relativamente suaves de saturación, por lo que la entrada ocasional en esos codos puede ser tolerable.
Además las señales habituales sólo manifiestan picos ocasionales. Así el factor de cresta del habla (diferencia entre el nivel pico y el nivel RMS) suele decirse que ronda los 12 dB, que ascienden a 18-20 dB para música. En consonancia con esto, es muy normal que los sistemas 'pro' tengan una holgura de 20dB por encima de esos +4dBu. Es decir, se diseñan para mantener una buena calidad (una distorsión baja) incluso cuando las señales llegan a niveles 20dB por encima del nivel de referencia pro +4dBu. Se espera que esas incursiones sean esporádicas, pero los sistemas las toleran sin mermar gravemente la calidad.
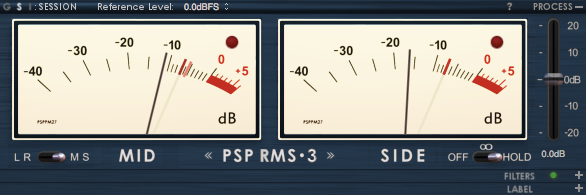
Tened también en cuenta que algunos sistemas software para medición de tipo vúmetro admiten configurar detalladamente algunos parámetros internos con lo que se distancian de la versión canónica de un vúmetro. Por ejemplo el TripleMeter de PSP que estamos mostrando en las imágenes admite definir a gusto el nivel de referencia, así como los tiempos de subida y bajada en cuanto a la reacción de la 'aguja', entre otros muchos parámetros editables. Una libertad que atenta contra el objetivo de 'estandarizar' las formas de medir, pero que a cambio puede a veces ayudarnos a investigar más a fondo qué sucede en algún tipo de señal o situación que enfrentemos.
Picómetros
Nos gusten más o menos, los ‘VU meter’ o ‘vúmetros’ son un estándar, y hay que acostumbrarse a usarlos con sus pros y sus contras. Entre los contras, el más evidente es el de que no muestran los valores pico ni las evoluciones vertiginosas en la señal, cosas ambas que son importantes en algunos tipos de situaciones y sistemas. En particular son esenciales en los sistemas digitales, por lo cual en ellos aparecen los picómetros, que sí representan valores pico.
En contraposición a los 'lentísimos' vúmetros, todavía en la çepoca analógica, aparecieron los PPM (Program Peak level Meters) que a pesar de su nombre no eran capaces de visualizar el pico verdadero de las señales. Se trataba más bien de vúmetros ágiles, con tiempo de activación en el orden de pocos milisegundos (una decena, por ejemplo). Los tiempos de desactivación, por el contrario, ascendían mucho, incluso por encima del segundo, para permitir que un pico breve quedara señalado el suficiente tiempo como para que el usuario no dejara de verlo.
A día de hoy, en sistemas digitales, sí tenemos posibilidades de representar el verdadero pico, no sólo como lo que correspondería a la muestra más alta sino incluso contando con las excursiones de la señal entre cada dos muestras (y que pueden llevar el pico a valores más allá de los presentes en las muestras). Sobre 'True peak metering: qué es y cómo usarlo' publicamos ya un tutorial que podéis revisar.
Pero eso es meternos ya en el terreno de definiciones y usos más modernos de los tipos de medidores para audio, con EBU R128 como ejemplo paradigmático y práctico del tipo de mediciones que se aplican hoy en las señales finales y en la masterización, y del que ya nos habló Euridia tiempo atrás en este artículo.
Algunas herramientas y plugins
Si queréis contar con un medidor capaz de operar en RMS, VU, PPM y EBU R128, podéis considerar el gratuito MV Meter de TB-Pro Audio, del que dimos referencia en esta noticia. Hay otros muchísimos, y es más que posible que vuestro DAW ya incorpore medidores de todo tipo. Por ejemplo Cubase cuenta desde la versión 8 con medidores en el master capaces de ofrecer datos conformes a EBU R128, además de otras medidas más clásicas tipo vúmetro.
También es justo nombrar PSP Triplemeter, del que hemos tomado las figuras que ilustran nuestro texto, el cual cuenta con medidores VU, RMS y PPM que podéis ver en este vídeo:
Presión sonora y sonoridad (III): curvas isofónicas (Fletcher-Munson) y de ponderación (A, B, C, K)
Habíamos dejado a propósito pendiente entrar un poco más en detalle en cómo la percepción del nivel audio es dependiente del tipo de contenido, es decir, de cómo sea la propia señal. No se perciben igual de fuertes señales del mismo nivel de energía pero que ocupen diferentes frecuencias, que tengan diferente reparto de la energía por las distintas zonas del espectro. Es más difícil oír los extremos (graves y agudos) que los medios. Nos generan una sensación de menor intensidad aunque se trate del mismo nivel de presión sonora (SPL).
Niveles típicos de presión sonora (SPL)
Y es que el nivel de presión sonora (SPL) mide realmente una característica física, no el cómo sentimos, a pesar de que muchas figuras y textos, leídos superficialmente, puedan llevarnos a pensar otra cosa.
El nivel 0 dBSPL corresponde a una presión sonora de 0,00002 Pa, que se suele considerar el umbral de audición pero que sólo lo es para señales que no residan en los extremos audio, sino en las octavas centrales (concretamente ese es el umbral a 1kHz). De forma parecida el nivel 120dBSPL suele considerarse un umbral de dolor (de nuevo para 1 kHz).
Los muchísimos gráficos y tablas (como la que aparece a continuación) que asocian a cada nivel SPL algún evento sonoro de la vida cotidiana contribuyen a extender ese mito de que el SPL mide de forma muy paralela a cómo oímos. Pero no es así. Mide, en el fondo, la presión sonora en el aire, no nuestra forma de sentir esa presión.
| Fuente | Presión sonora (Pa) | dBSPL |
| Cohete | 100000 | 195 |
| Junto al reactor de un avión | 6300 | 170 |
| Avión a reactor grande | 2000 | 160 |
| Avión a reactor medio | 630 | 150 |
| Avión a hélice | 200 | 140 |
| Golpe en tutti de orquesta con 80 músicos | 63 | 130 |
| Martillo neumático | 20 | 120 |
| Gran sistema de ventilación | 6.3 | 110 |
| Autopista, imprenta | 2 | 100 |
| Camión pesado a 6 metros, manifestación con griterío | 0.63 | 90 |
| Calle con tráfico intenso, oficina ruidosa | 0.2 | 80 |
| Equipo audio doméstico | 0.063 | 70 |
| Conversación (a 1 metro) | 0.02 | 60 |
| Zona urbana tranquila, de día | 0.0063 | 50 |
| Zona urbana tranquila, de noche | 0.002 | 40 |
| Habla a muy bajo nivel | 0.00063 | 30 |
| Ruido en un estudio de grabación | 0.0002 | 20 |
| Persona susurrando débilmente | 0.000063 | 10 |
Umbral de audición
| 0.00002 | 0 |
Tened en cuenta que esta tabla es toda ella muy 'ficticia' -como cualquiera parecida- y sólo al efecto de dar una idea de rangos
Este carácter sólo aproximado no resta utilidad a que tengamos en la memoria alguna correspondencia de este tipo para los valores SPL, aunque sí relativiza su valor. De hecho no suenan igual de fuertes todos los camiones ni aeronaves, habría que considerar también a qué distancia estamos de esas fuentes, etc. Está claro que son referencias sólo ilustrativas.
Además, y eso es de lo que nos vamos a ocupar hoy: cómo en función de la propia estructura de la señal se afecta al nivel percibido.
Enmascaramiento temporal: ¿viva la novedad?
Por empezar con algo que no está en el título de hoy, un ejemplo claro de dependencia de la escucha con la propia señal son los fenómenos de enmascaramiento temporal. Lo que escuchamos viene influenciado por lo lo que hemos escuchado inmediatamente antes. Fenómenos que por otra parte son comunes al resto de los sentidos. El mal olor de una cloaca lo es menos si llevamos en ese ambiente unos minutos, nos acomodamos a lo que nos ofrece el entorno y pierde protagonismo en nuestra percepción para dejar hueco a recibir nuevos estímulos (que quizá apunten a la llegada de algún nuevo peligro). De forma parecida un sonido estático que se mantiene largo tiempo puede ser molesto pero muchas veces acaba pudiendo ser obviado.
Un ruido estático es menos notorio que un ruido variante que está constantemente reclamando atención sobre su evolución, hasta el punto de aparentar menor nivel. Y no es igual de molesto ese sonido estático si se trata de ruido blanco (muchas veces admisible, al menos a bajo nivel) o si es una interferencia tonal o señal cíclica (bastante incordiante aunque haya presencia de otras señales mucho más fuertes).
Pero por fenómenos de enmascaramiento también nos referimos a otros que actúan en sentido contrario, que en lugar de apoyar ‘lo novedoso’, parecen dispuestos a ‘tapar’ la novedad. Por ejemplo la presencia de un sonido fuerte puede hacer menos audibles los sonidos débiles que vienen inmediatamente detrás, siempre y cuando no sean sonidos muy diferentes sino que ofrezcan una configuración espectral parecida (de otra forma el efecto 'novedad' dominaría en su percepción).
Una de las razones es que la forma de poder atender en el oído al enorme rango de unos 120dB que separa los sonidos más débiles y los más fuertes pasa por contar con mecanismos que ‘endurecen’ la audición ante grandes presiones. La cadena de huesecillos que en un ambiente sonoro tranquilo está relajada y es muy sensible, en cierta manera se ‘previene’ con la llegada de niveles fuertes y dificulta la transmisión para protegerse. En una escala de tiempo mayor, también cuando pasamos un rato largo en un ambiente de fuerte presión sonora, como una actuación de música pop/rock o una discoteca, la capacidad de escuchar se queda trastornada y tarda en recuperar su sensibilidad normal.
Pero en esos efectos de enmascaramiento, especialmente cuando se trata de escalas temporales cortas, hay mucha intervención también de cómo el cerebro interpreta los estímulos que el oído le envía. Por ejemplo un sonido ‘fuerte’ tras uno débil puede hacer parecer más corto el primero. Hay un sinfín de ilusiones sonoras de este tipo que nos hablan del papel esencial de la parte ‘interpretativa/cerebral’ en la audición.
Más allá de juegos de laboratorio con señales muy atípicas que provocan esas ilusiones sonoras, lo más normal es que el enmascaramiento suceda de forma que lo pasado puede enmascarar lo futuro, y sólo en mucho menor medida al revés.
Por ejemplo estamos acostumbrados a oír los sonidos en entornos que reverberan en mayor o menor medida y por tanto que haya ‘colas’ en las que el sonido se amortigua al parar de producirse es algo esperado y que no llama la atención. Pero cualquier fenómeno de tipo ‘pre-eco’ resulta ser por comparación muy llamativo, capaz de alterar el carácter y nitidez de una señal mucho más que un post-eco. Lo mencionamos ahora porque más adelante tendremos ocasión de ver que hay sistemas que al tratar señales acaban generando algunas dosis de pre-eco.
No ahondaremos más sobre estas cuestiones de enmascaramiento temporal, porque nuestro interés principal hoy está en presentar cómo percibimos la sonoridad en función de la frecuencia, algo estudiado hace ya larguísimo tiempo por Fletcher y Munson.
Curvas isofónicas de Fletcher-Munson
Fletcher y Munson estudiaron estadísticamente cómo oímos a diferentes frecuencias, a base de anotar las respuestas de un amplio grupo de personas antes señales de prueba. Es muy fácil apreciar que oír dos tonos diferentes con el mismo nivel SPL, como por ejemplo 200 y 1600 Hz, produce sensación de un nivel percibido muy diferente (mucho mayor en el de 1600).
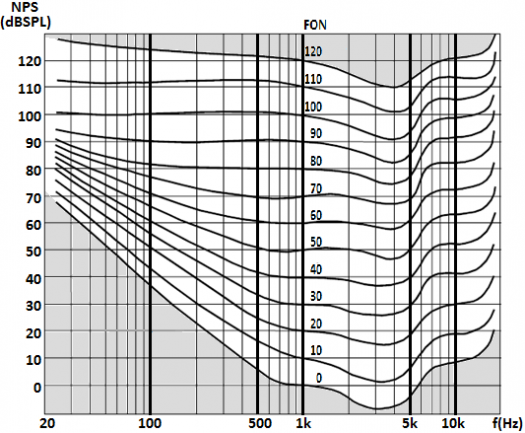
Tuvieron la idea de crear unas ‘gráficas de igual sonoridad’ (curvas isofónicas) para diferentes niveles, desde muy cercanos al umbral de audición a otros ya realmente fuertes. Cada curva representa el nivel de presión sonora (SPL) que hay que producir a cada frecuencia para conseguir una misma sensación que la que se tiene con un determinado nivel a 1kHz. Tomando como referencia el recorrido entre los umbrales de audición y dolor a 1kHz (0 y 120 dBSPL) crearon curvas cada de sonoridad igual a un tono de 1kHz y nivel 0, 10, 20, 30, … etc dBSPL. Las curvas provienen de promediar las respuestas en tests de un amplio grupo de personas.
Las curvas Fletcher-Munson son un clásico, y aunque estudios más recientes revelan algunas diferencias, las tendencias que marcan siguen siendo válidas. Así que centrémonos en entender qué información útil nos proporcionan.
Algunas conclusiones a partir de las curvas isofónicas
- Desde 1500 hasta 6000 Hz, aprox. , tenemos mayor sensibilidad, con 3000 Hz. como la frecuencia más sensible.
- Salvando esa zona siempre un poco más sensible, por debajo de 600 y por encima de 6000Hz tenemos cada vez más dificultad para escuchar, tenemos menor sensibilidad
- En la parte alta (más de 6000Hz) se trata principalmente de un ‘escalón’ (con unos 10dB menos de sensibilidad que a 1000Hz.) acompañado del efecto de desaparición progresiva de la escucha de los muy agudos (15000 en adelante) que es muy severo. Pero globalmente el recorrido dinámico (salvo en esas altísimas frecuencias que ya se pierden) apenas se ha reducido, siendo de unos 110 dB en vez de 120
- En la parte de bajas frecuencias tenemos efectos mucho más severos, con una compresión progresiva del rango dinámico que llega a ser de sólo 60 dB (la mitad) frente a los 120 presentes a 1000Hz.
- Esa compresión del rango dinámico de los graves se produce sin apenas variar el nivel de dolor: todo se concentra en una pérdida de capacidad de escuchar que eleva los umbrales de audición a esas frecuencias y compacta todas las curvas acercándolas, haciendo por tanto que en esas regiones graves los ‘saltos’ de potencia necesarios para incrementar la presencia de sonido percibida sean menores de lo que cabría esperar (hablo de los ‘saltos’, porque los niveles absolutos son siempre mucho mayores).
- Conviene destacar también el que la parte de altos niveles es, comparativamente, mucho más ‘plana’, con una sensación mucho más ‘equilibrada’ en el sentido de que corra pareja al nivel de presión sonora sin demasiados altibajos según se trate de unas u otras frecuencias.
Podéis pensar en cómo reexpresar esas observaciones en conclusiones útiles.
Estas curvas son las que están, por ejemplo, detrás de los circuitos ‘loudness’ de muchos sistemas hifi y car-audio. Hay distintas versiones (más avanzadas y menos) pero en los buenos se imparte un refuerzo en graves y en agudos sólo cuando estamos reproduciendo a niveles medios y bajos, pero ese retoque no se aplica cuando estamos reproduciendo a niveles altos. Eso facilita la escucha ‘equilibrada’ a cualquier nivel, y nos permite escuchar ‘mejor’ sin necesidad de tener que subir el volumen para poder oír los graves y agudos.
Las implicaciones que subyacen en estas curvas impactan también en muchas decisiones que hemos de tomar, por ejemplo sobre a qué niveles conviene mezclar o trabajar en edición audio. Mezclando a niveles más bajos de los que vayan a ser los niveles de escucha que usen los destinatarios finales, percibiremos reforzados los medios (tendremos mayor sensibilidad a esa zona). Eso podría significar (si no lo tenemos en cuenta) que una mezcla aparentemente equilibrada y biensonante a nuestro nivel de escucha durante la mezcla, suene para los que lo escuchen a niveles mayores desequilibrada con una significativa carencia de medios. No creo que nadie (tampoco yo) os recomiende usar en esos casos el ‘loudness’ al que antes me refería, porque es una escucha engañosa. El preferible oír mal pero con defectos conocidos, y lo del ‘loudness’ es, las más de las veces, un terreno de magia poco confiable.
Como no sabemos a qué nivel se va a escuchar por el destinatario final (a veces sí, si se trata de cine, ferias, instalaciones audivisuales, etc.), tiene este problema difícil solución. Incluso si supiéramos a qué nivel se van a oír nuestras producciones, seguramente no desearíamos pasar horas y horas de trabajo a unos niveles tan altos como los que se estilan hoy día (en cines, clubs, o incluso por los particulares con sus MP3 y auriculares). De ahí la importancia de aprender a escuchar a distintos niveles durante una producción. Personalmente, me gusta ser respetuoso con mis oídos y no trabajar a niveles fuertes, tiendo a buscar la escucha a niveles más bien bajos. Pero de cuando en cuando hay que oír cómo van los resultados a otros niveles más altos para no perder perspectiva.
Una persona entrenada puede ‘aprender’ esas diferencias y le bastará escuchar sólo ocasionalmente a niveles medios/altos para quedarse con una huella en su memoria de cómo están sonando las cosas, Huella que le permitirá seguir trabajando, a unos niveles menores, sabiendo qué tipo de compensaciones tiene que ir realizando.
Además es una sana costumbre esa de ‘refrescar’ el oído con cambios, para que no se acomode a oír siempre de una misma manera y se mantenga atento. Esa es la razón de que de vez en cuando, durante una sesión de trabajo, debamos escuchar otras cosas: grabaciones en ese mismo tipo de estilo/producto (para tener referencias de cómo ha de sonar muestro resultado), o incluso escucha de sonidos que nada tengan que ver para una cierta ‘limpieza’ regular del oído (por ejemplo a mí me gustan especialmente a este respecto buenas grabaciones de sonidos de costa con el romper de las olas tan generoso en ancho de banda y en imagen estéreo). Pero es también beneficioso realizar cambios de nivel en la escucha del material que estamos trabajando.
Tenéis algunos consejos más e interpretaciones prácticas del significado de estas curvas, cara a la sonorización en vivo (algo bien diferente a la cuestión de la mezcla) en: https://www.hispasonic.com/reportajes/jugando-psicoacustica-ii-fletcher-munson/40662
Pero sobre todo lo que debéis es recordar las tendencias principales a las que estas curvas apuntan, para estar prevenidos y saber compensar cuando se necesite ese comportamiento auditivo inevitable.
Otras curvas isofónicas
Por más que conocidas, las de Fletcher y Munson (creadas en la década de 1930) no son las únicas curvas de este tipo que existen. Ha habido otros muchos tests con sus propias conclusiones (como los de Robertson y Datson en los años 1950, que diferían bastante, pero que han sido posterioremente desaconsejadas) e incluso se han estandarizado en normas ISO diferentes versiones de curvas isofónicas a lo largo del tiempo.
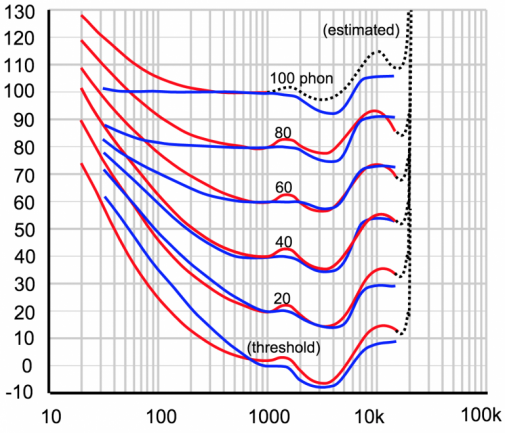
La propia ISO redefinió sus curvas isofónicas en 2003, y en este gráfico podéis observar una comparativa entre las curvas de Fletcher-Munson (en azul) y las definidas por ISO (en rojo, y extendidas por estimación en línea de puntos).
Si tomamos las curvas de la norma ISO 226:2003 como buenas (más recientes, con mejores medios para los tests, etc.), hay diferencias significativas especialmente en la zona siempre crítica de los graves. Fijaos que las curvas ISO apuntan a una reducción aún mayor del margen dinámico respecto al que señalaban Fletcher-Munson.
Curvas de ponderación A, B y C: hecha la ley, hecha la trampa
Como respuesta técnica al problema al que apuntan las curvas isofónicas, se han definido unas curvas en frecuencia que, usadas como filtro delante de un equipo de medida o representación (que por sí mismo es mucho más ‘plano’ es su respuesta y no tiene esas diferencias a las que apuntan las isofónicas) hacen que la señal que llegue al sistema de medición/representación venga coloreada de forma parecida a como estaría coloreando nuestra percepción. Curvas que 'imitan' la forma en la que sentimos el nivel de los sonidos con el objetivo de poder ofrecer mediciones que sean algo más útiles que la medida directa sobre la señal original.
Más que definirse por una extrema fidelidad a los contornos isofónicos, se ha pretendido con ellas un filtrado sencillo y fácil de realizar, que sólo aproxime las tendencias principales en las curvas isofónicas, las cuales, al fin y al cabo son sólo un promedio estadístico de lo que cada uno de nosotros percibe.
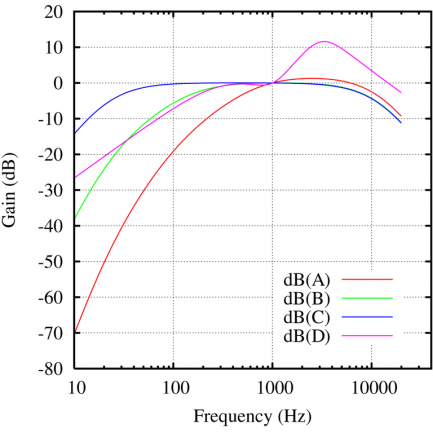
Son tres curvas definidas en la norma ANSI S1.4-1971 y pensadas para aplicarlas a diferentes ‘intensidades’ de señal. Grosso modo, la curva A invierte la curva isofónica de 40 fons, la B correspondería a 70 fons y la C a 100 fons. Típicamente la que más se usa es la A, que por ser la que se aplica para niveles más pequeños es la que impacta más fuertemente en el resultado (es la que tiene una acción de filtrado más decidida).
La curva A se usa cuando el sonido que se analiza va a estar presente a niveles bajos, en los que la escucha tiene una enorme pérdida gradual hacia los graves y una bajada de unos 10 en agudos. Sería habitual aplicarla al medir un ruido ambiente o un ruido de fondo en un equipo electrónico, porque se trata de ruidos típicamente de poco nivel. La medida física en dBSPL resultaría más alta de la sensación que tendríamos en FONS, y la aplicación de la curva A intenta paliar eso.
La curva B se aplica al estudiar señales que tienen niveles medios, y es habitual para medir contenidos musicales, por ejemplo. Mantiene un rebaje de la zona grave pero no tan profundo como la A.
La curva C se aplica para señales fuertes, y es la más plana de las tres.
Hay también una curva D que sólo se aplica ante ruidos realmente feroces, como los de aeronáutica y que respecto a las otras destaca porque enfatiza la parte de altas frecuencias.
Una crítica general a todas estas curvas es que han sido obtenidas a partir de señales de prueba sinusoidales, que son muy diferentes a las señales que típicamente se manejan en audio. Como respuesta ha habido otras muchas propuestas de sistemas y curvas de ponderación desde la ISO, EBU y otras entidades.
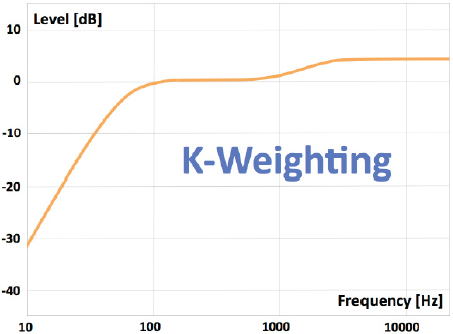
Más recientemente ha surgido también la curva K, de uso en en ITU BS.1770 y EBU R-128, que introduce una caída en graves (mediante un filtro paso alto) y un refuerzo en agudos (mediante un filtro de tipo escalón o shelving).
Por contraste con estas curvas, a veces se habla de curva Z para referirse a una respuesta plana entre 10 Hz y 20 kHz (sin ninguna ponderación).
Los db..(A), db..(B), db..(C), dB..(K)
La aplicación de las curvas puede hacerse ante muchos tipos de medición, no sólo de nivel de presión sonora, sino también en las señales eléctricas que entran o salen de un equipo, el ruido de fondo que este genera, etc.
En caso de aplicarse alguna de estas curvas, la unidad correspondiente (típicamente algún tipo de dB-algo, como dBSPL en presión sonora, o dBV o dBu en el caso de señales audio eléctricas) se acompaña de A, B o C entre paréntesis dando lugar a cosas como dBSPL(A), dBSPL(B), dBSPL(C), dBV(B), etc. Es importante recordar lo que esto implica en la medida cuando veamos cifras señaladas de esta forma.
Por ejemplo, muchos fabricantes aplican en ciertos tipos de medida la ley A porque el resultado que se obtiene (con un valor menor al ser la que más reduce la presencia de componentes graves) les resulta beneficioso, por ejemplo con una cifra de ruido que aparenta ser menor. No es ningún intento de engaño, si estamos convenientemente informados de lo que esto representa. Otras veces veremos que nos ofrecen las mediciones con y sin ponderación, lo que resulta mucho más transparente.
De hecho ha habido y hay un cierto abuso (incluso exigido en algunas normas) de la ley A, que acaba siendo aplicada a todo tipo de mediciones aunque se trate de señales fuertes.
Otras siglas se han ido generando que tienen su propio significado. Así por ejemplo en digital podremos encontrar LKFS (referido a loudness k-weighted full scale), una escala en dB definida en ITU BS.1770, y que la EBU R-128 denomina LUFS (loudness units full scale). En otro momento podremos presentar R-128 con algo más de detenimiento, pero podéis encontrar también muchas aclaraciones a partir de este enlace de tcelectronic.como, si no os asustan lecturas más técnicas y menos divulgativas, directamente en los propios documentos de la EBU.
Artículo publicado por Pablo F. Cid en https://www.hispasonic.com/tutoriales/presion-sonora-sonoridad-iii-curvas-isofonicas-fletcher-munson-ponderacion-b-c-k/43351



No hay comentarios:
Publicar un comentario