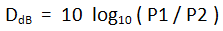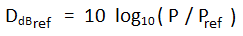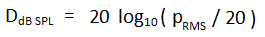Decibelios a secas (dB) y con apellido (dBm, dBW, dBSPL...)

Hoy distinguimos los dB a secas y los ‘dB-algo’ como pueden ser dBm, dBW, dB SPL, dBV, dBu, dBFS y tantísimos otros que vemos desfilar a diario. Afortunadamente una diferencia sencilla de entender pero que pese a ello no todos tenemos clara y ocasiona en más de una ocasión conflictos de interpretación.

[Nota: Si necesitáis recordar qué significa esto de los dB podéis revisar un tutorial anterior.]

dB para todos los gustos

pablofcid

Los dB (relativos) y los dB-algo (absolutos)

El valor D (en dB) que corresponde a una determinada relación entre dos potencias se describe como:

Los dB 'sin apellido'

pablofcid

siendo P1 / P2 el cociente entre dos potencias expresadas en la misma unidad.

Típicamente se trata de la potencia P1 a la salida de un sistema o cable cuando atacamos su entrada con una potencia P2. El cociente P1/P2 describe así cuántas veces mayor o menor es P1 respecto a P2. Esa definición corresponde a los dB 'sin apellido'. Estos dB 'a secas' se usan para caracterizar relación salida/entrada de un sistema(caracterizar su ganancia o pérdida en potencia).

Una definición muy parecida es la que existe cuando usamos este mismo tipo de fórmula para valorar una cierta potencia frente a otra prefijada y conocida de antemano que tomamos como valor de referencia:

Los dB 'con apellido'

pablofcid

Estos ‘dB-algo’ se usan para medir cantidades por comparación con una cantidad fija que tomamos como referencia. Son los que llamo los 'dB con apellido' o los ‘dB-algo’, porque no se describen como dB sin más, necesitan acompañarse de la indicación de la referencia usada. Así, por ejemplo, los dBm usan el mW (milivatio) como referencia o los dBW el W (vatio).

No tiene nada que ver un uso con otro, y por eso he querido destacarlo en este tutorial. El parecido es formal (la fórmula que se usa para calcularlos) pero en semántica y en uso tienen sus diferencias de las que conviene ser consciente. Comparten una misma forma de representación 'a lo dB' (lo que implica una representación relativa y logarítmica de la que hemos hablado en otro tutorial, al que os recomendamos ir si no tenéis claro qué son los dB o su fórmula) pero tienen demasiadas diferencias como para obviarlas.

dB sin apellido

La definición de los dB 'a secas' carece de unidades, y en ese sentido casi diríamos que no sirve para medir 'absolutamente' nada. Lo digo con truco: no mide nada 'absoluto' porque sólo mide algo 'relativo'. No puede expresarse con ‘dB’ un valor de una magnitud o variable (como pueden ser X vatios, X gramos, X pascales, o lo que os apetezca), pero sí mide la ganancia o pérdida de un sistema porque compara el valor de una magnitud a su salida y a su entrada. Un valor en dB sólo mide cuánto crece o decrece algo, no establece un valor concreto.

Es de hecho así como nacieron, vinculados a la necesidad de expresar de una forma práctica la ganancia o pérdida que sufre la potencia de una señal al atravesar un sistema o un medio de transmisión. Por ejemplo miden qué ganancia aplica un amplificador o qué pérdida impone un cable o un conector porque estudia cuántas veces más grande o más pequeño es la potencia que hay a la salida respecto a la que entró, es siempre una medida comparativa. En la fórmula para calcular los dB aparece siempre un cociente entre dos cantidades. Ese cociente implica dos cantidades homogéneas (de la misma unidad) y por tanto es adimensional: una medida en dB no tiene unidades, en reflejo evidente de que no ‘mide’ otra cosa que la proporción o relación que guardan esas dos cosas entre sí.

Cuando escribimos 50 m. o 22 kg. estamos reuniendo una cifra y su unidad. Cuando escribimos 12 dB el indicativo ‘dB’ no es una unidad aunque lo parezca, aunque tenga la apariencia de serlo. Acompañamos el valor numérico del indicativo ‘dB’, pero en realidad habla de un cociente adimensional. Al escribir dB (a secas, sin apellido) acompañando a la cifra, realmente sólo indicamos que ese cociente no lo estamos ofreciendo con su valor tal cual, sino sometido a la transformación/representación logarítmica que implica el uso de los decibelios.

dB con apellido

Los dB con apellido sí permiten medir y describir cantidades absolutas. Cantidades absolutas y por supuesto en las que existe y es conocida la unidad que estamos usando.

Con los dB-algo no se trata de observar el cambio o la relación entrada/salida de un sistema, sino de describir un valor comparándolo con otro prefijado que se toma como referencia. Para poder usarse para describir cantidades absolutas el truco está en que la relación se establece con esa cantidad fija y conocida de antemano. Ejemplo evidentísimo son los ya referidos dBm (usan el mW como referencia) y dBW (medidos respecto al vatio).

De esa forma el cociente mide la proporción que guarda una cantidad con otra que se toma como referencia. Los ‘dB-algo’ sí miden cantidades absolutas y sí implícan cierta unidad. Una unidad que queda finalmente explícita a través de ese necesario apellido que en esos casos va junto a dB. Lo entendemos a la perfección con dos de losejemplos más triviales de db-algo:

Los dBW o ‘decibelivatios’ describen un valor en vatios pero no por su valor original (los vatios tal cual) sino usando la representación ‘dB’ para aprovechar sus ventajas (recorrido más compacto, etc.). Los dBm o 'decibelimilis' usan como referencia el milivatio, haciendo más útil esa unidad dBm para caracterizar potencias pequeñas. Por tanto los dBW y los dBm son en el fondo cantidades que expresan W y mW, pero en lugar de su enorme recorrido con muchísimas cifras reexpresado en el pequeño rango de valores a que da lugar el paso a la representación en dB (típicamente de céntimas hasta poco más de una centena).

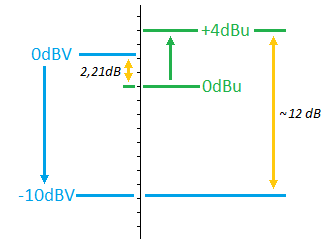
Pero no siempre es todo tan sencillo como en estos dos ejemplos en los que directamente veíamos aparecer el W o el mW (unidades muy habituales en sí mismas dentro de la física común). Es el caso de un tipo de dB-algo bien conocido por la gente que trata con la acústica y la sonorización, y que también veréis en las especificaciones de muchos monitores y cajas de altavoces, y que tomamos como excusa para seguir profundizando en el entendimiento de los 'dB-algo'.

Un ejemplo interesante: el nivel de presión sonora o dB SPL

Los dB SPL (por 'sound pressure level' o nivel de presión sonora) no usan como referencia una unidad del sistema internacional como el W, ni ninguna otra típica como el mW. Los dB-algo permiten tomar cualquier referencia que nos sea útil. En el caso del nivel de presión sonora, lo que se ha tomado como referencia es el umbral de la audición humana. Un valor establecido por la práctica, por estadísticas y pruebas con oyentes, y que representa en el fondo el mínimo murmullo sonoro que somo capaces de oír. Ese umbral está fijado (aunque distintas personas puedan diferir, es una media aceptada) en una presión acústica de 20 micropascales.

SPL una medida relativa al umbral de audición

donde el p (RMS) que va en el numerador del cociente es la presión acústica eficaz (RMS) en micropascales.

Se ha escogido esa referencia porque así 0dB SPL implica un sonido apenas perceptible: menos que eso directamente no se oye. Y es que hasta los ingenieros huyen de complicarse la existencia con los números: de un plumazo se han quitado los posible valores negativos. Además, elegido de esa forma, con una referencia que tiene un significado práctico (no una mera unidad del aséptico sistema internacional) los ingenieros y también nosotros podemos dedicarnos a pensar en términos prácticos y sin liarnos por qué significa la presión acústica o el micropascal.

Es la ventaja del uso del dB SPL (como lo es de otros dB-algo): aunque no conozca qué es un micropascal o ni siquiera qué narices es la presión acústica, sí puedo imaginar qué significa 'el mínimo audible' y esta medida 'SPL' nos da la ratio respecto a esa cantidad. Por ejemplo podemos comprender que 20 dB SPL implican una potencia (recordad que los dB siempre hablan de 'potencia') que es 100 veces superior al mínimo y que para muchos de nosotros sigue siendo un grado de silencio deseable pero muy pocas veces alcanzable. Cuando nos dicen que una sala tranquila se mueve en torno a 40 o 50 dB SPL o que un tutti orquestal llega por encima de los 100 dB SPL, lo entendemos y asociamos significados prácticos a los valores en dB SPL. Especialmente si también sabemos que 120 dB SPL es un nivel que se tilda ya de doloroso (al menos si se mantiene un tiempo) y que por encima puede haber daños al oído.

Poco nos importa (fijaos que lo digo ahora, cuando más o menos ya nos parecía que entendíamos algo respecto a los dB SPL) que la presión sonora, a pesar de que la haya escrito con 'p' sea una unidad de campo y no de potencia (para que lo entendamos mejor: no mide potencia sino 'amplitud' o 'nivel'). De hecho por eso usé una 'p' minúscula, para que no la confundamos con una potencia que en las primeras fórmulas siempre estaba señalando con 'P' mayúscula.

[Nota: Los que, comprensiblemente, os liéis con esto de la amplitud o la potencia y su efecto sobre la cuestión de los dB tenéis otro tutorial en el que os explico específicamente esa cuestión, y que es lo que da lugar a que la fórmula de los dB SPL arranque con un 20 delante del logaritmo y no con un 10]

Artículo de Pablo F.Cid publicado en www.hispasonic.com

https://www.hispasonic.com/tutoriales/decibelios-secas-db-apellido-dbm-dbw-dbspl/43045

Qué son los niveles de línea -10dBV y +4dBu

Describimos los dos niveles de voltaje típicos en señales de línea (-10dBV ‘doméstico’ o ‘consumo’ y +4dBu ‘profesional’), la diferencia de casi 12 dB entre ellos, y la relación algo difusa que guardan con los 0dBm. En otra entrega, una vez tengamos claro qué significan estos niveles, hablaremos de los márgenes (headroom) en las conexiones, la interconexión entre sistemas, y también de la relación con los VU típicos en analógico y los dBFS típicos en digital (dB 'a fondo de escala').

Si lo necesitas, puedes repasar el tutorial sobre qué son los dB contado para músicos, así como otro sobre los dB ‘a secas’ frente a dB con ‘apellido’ (como estos dBV y dBu). De la cuestión de cómo los dB (una representación ideada para hablar de potencias) puede aplicarse a algo que habla de amplitudes ya hemos publicado también un tutorial.

Resumen para quienes tengan prisa

En concreto estos dos estándares corresponden a estas tensiones:

• -10dBV definen una señal de 0,316 V RMS (senoidal de 0,443 V pico)
• +4 dBu definen una señal de 1,23 V RMS (senoidal de 1,74 V pico)

Por tanto la salida profesional aporta un nivel de tensión 4 veces mayor (aprox.) que la doméstica, lo que implica una potencia 16 veces mayor, que no es poca cosa como apreciamos al indicar ese salto en dBs:

• Hay aprox. 12 dB de diferencia entre ambos niveles

Si sois de los que queréis utilidad práctica en todo cuanto leéis, esa última cifra os da también una primera idea simple de cómo equilibrar conexiones entre uno y otro nivel: asegurando esa diferencia de 12 dB con algún atenuador (si vais de salida ‘pro’ a ‘consumidor’, típicamente bastará bajar el nivel de salida para situarlo en -12dB) o con algún pequeño amplificador previo si vais de salida ‘consumo’ a ‘pro’ para darle ese salto (de lo contrario perderéis 12 dB de calidad SNR, aunque también es cierto que un producto ‘consumo’ seguramente no tenga el nivel de calidad de un ‘pro’ y por tanto no se consiga finalmente mejor calidad aunque elevéis esos 12dB, todo es cuestión de comprobar la SNR de origen, la que os ofrece el producto ‘consumo’, respecto a la disponible en el ‘pro’).

Pero, como os anunciaba, en una entrega posterior haremos mención más detallada a la cuestión de la interconexión, en la que puede profundizarse bastante más allá de esta regla básica y un tanto simplista de los 12 dB.

Detalle de un interfaz Tascam US-16x08

tascam.com

Referencias en voltaje o en potencia

Tal como veremos, en la definición de los dBV y de los dBu interviene una mención a la potencia de 1mW, así que antes de ir a por nuestros niveles de línea audio, pensemos por un momento en cuestiones de potencia. Eso nos permitirá llegar a asociar los dBV y los dBu (que hablan de tensión) con los dBm (que miden potencia), aunque, como veremos, no será una relación ‘fija’ sino dependiente de la carga

Distinguir potencia y voltaje es importante. Un ejemplo: En el enchufe hay siempre una tensión (los famosos 220V AC) pero mientras no enchufamos una carga no circula corriente y no se consume ninguna potencia. Un horno microondas suele ser de potencia aprox. 800W porque para realizar su función absorbe mucha corriente, mientras una pequeña lámpara LED para lectura es de unos 5W y sólo exige el paso de una corriente muy pequeña. Es decir: en función de cuál sea la carga, la potencia que se desarrolla es una u otra, pese a que el voltaje sea el mismo.

Algo parecido pasa con nuestros equipos audio. Muchas veces nos interesa de los sistemas su potencia más que su puro nivel de amplitud o voltaje, porque es la potencia la que habla del trabajo que desarrollamos con esos sistemas.

Pero cuando hablamos de señales la cosa cambia. Una señal en sí no tiene ‘potencia’. La señal, entendida como la ‘forma’, está en nuestro caso definida por el voltaje que representa al sonido. Cuando hablamos de niveles de señal y de interconexión de sistemas es normal por tanto que nos interesemos por los voltajes, mientras que cuando hablamos de la capacidad de un sistema para generar acciones nos interesa más la potencia.

Sin carga no hay potencia: ¿cómo medir una salida entonces? El dBV y el dBu

Nadie habla en un ampli de la tensión que generan, sino de la potencia, de sus vatios. Esa potencia que viene en la hoja de especificaciones está vinculada a usar cajas altavoces de cierta carga o impedancia: genera X vatios sobre carga de 8 ohmios (y otra distinta sobre carga de 4 ohmios).

Para caracterizar una salida (como la de un micro o un previo) y poder hablar de ella con independencia de cuál sea el sistema al que vayamos a conectarla, no podemos usar potencia. Sencillamente porque no se puede valorar qué potencia se desarrollará sobre una carga desconocida. Es por ello que se ha decidido aplicar unidades que hablan de relaciones entre tensiones.

Así, los niveles de las salidas audio estándar son -10dBV y +4dBu. Las unidades dBV y dBu no miden relaciones entre potencias, no están directamente relacionadas con los W o mW, ni por tanto con los dBW ni los dBm. Están definidas como relaciones entre voltajes. Nos hablan del voltaje nominal de la salida. Sólo conociendo la impedancia de la carga que vaya a usarse podrían hacerse correspondencias a potencias.

Una impedancia de carga exageradamente baja podrá hacer inservible el sistema, porque la salida no pueda alimentar tanta corriente como exige esa carga y entre en severa distorsión. Pero ese no es el problema del que hablan los dBV y los dBu, que sólo quieren servir para que sepamos qué nivel de señal (qué nivel de voltaje) vamos a encontrar cuando las cosas funcionen bien (no con cargas anormalmente bajas).

Lo curioso es que tanto el dBV como el dBu, pese a saber que hablarán de voltajes, se definieron tomando como modelo qué potencia desarrollaría ese voltaje sobre cierta carga. Buff…. Ánimo que ya mismo deshacemos el lío.

+4dBu y -10dBV los dos estándares de nivel línea

Imagen tomada del manual de un

El nivel audio ‘doméstico’

Qué son 0dBV

Fijaos que empiezo por hablar de 0dBV y no todavía de los -10dBV que definen al nivel línea ‘doméstico’.

El nivel 0dBV se definió como el que corresponde a una senoide cuya tensión RMS (o eficaz) sea de 1V (RMS). Esa tensión senoidal de 1 V RMS de la que habla 0dBVaplicada a una resistencia de 1kOhmio implicaría una potencia de 1 mW, o lo que es lo mismo 0dBm.

Pero eso es sólo un caso entre los muchos posibles porque la carga podría ser diferente a 1kohmio y la forma de onda podría no ser senoidal. Veis que hay cierta asociación un poco débil con una ‘potencia’: 0dBV con una resistencia de 1kOhm generaría 1mW, o sea 0dBm. Genial: los dBV y los dBm coinciden… Sí, pero sólo si la carga es de 1kOhm. Menos es nada, al menos nos da una idea de por dónde puede andar.

Se definió así por simplicidad: 1V (RMS) es algo fácil de medir y de recordar, lo mismo que son fáciles de recordar 1 kOhmio y 1 mW. Son valores ‘razonables’ en el ámbito de pequeña señal. Pero no olvidéis que sobre otra impedancia que no sean los 1000 Ohm sería distinta la potencia que se generaría, claro. Y es que con los dBV lo que nos importa realmente medir es el nivel de voltaje, no la potencia. 0dBV equivale a hablar de 1V RMS.

Ya os comenté que me gusta pensar también en picos: una senoidal de 1V RMS tiene unnivel de pico de 1,4V aprox.

-10dBV son 0,316 V RMS o 0,443 V pico (senoidal)

Finalmente ¿Qué son -10dBV? Partiendo de la tensión 1V RMS que representan los 0dBV, y como -10dB corresponden a una relación 0,1 en potencia y por tanto a una relación 0,316… en amplitud (raíz cuadrada de 0,1), llegamos a que

• -10dBV corresponden a una senoide de 0,316 V RMS o 0,443 V pico

En cuanto a potencia, si asociamos 0dBV a 0dBm (1mW) está claro que -10dBV corresponderá a -10 dBm (0.1mW, realmente muy poca potencia), pero de nuevo sólo valdría considerando impedancia de 1000 Ohm y señal senoidal.

• -10dBV son 0.1mW sólo cuando la carga es 1000 Ohm y la señal senoidal

Sobre cualquier otro tipo de carga o señal serían otros valores de potencia en mW, pero siempre -10dBV sería 10 veces menos potencia que 0dBV. Por si en algún momento necesitáis relacionarlo con potencia, nos puede quedar la idea de que con cargas que ronden los 1000 Ohm hablar del estándar -10dBV es hablar de 0.1mW ante señal senoidal (3dB más con cuadrada). Si la carga rondara los 100 Ohm (cuanta menor carga mayor potencia en una relación que es lineal) volveríamos a tener 1 mW: la carga ha bajado diez veces, y por tanto la potencia ha subido en esa misma proporción. Si la carga fuera de 10kOhm tendríamos una potencia de sólo 0.01W.

La vinculación entre tensión y potencia, entre dBV y dBm, es por lo tanto muy leve. Totalmente dependiente de la carga (o impedancia) así como de la forma de la señal que estemos considerando, y que muy pocas veces va a ser senoidal salvo en pruebas de laboratorio. Pero es que en este ámbito ya decíamos que no es la potencia lo que nos interesa caracterizar, sino el nivel de las señales, su amplitud.

El nivel audio ‘profesional’

Qué son 0dBu

Vamos también aquí a empezar por pensar no en los +4dBu sino en la referencia 0dBu.

0dBu se ha definido como el voltaje que hace falta tenga una senoide para que sobre una carga de 600 Ohm genere 1mW (o lo que es lo mismo 0dBm). Y resulta ser unasenoide de 0,775 V RMS que correspondería a un voltaje de 1,1 V pico. Fijaos que, curiosamente, es ¡más bajo! que el que correspondía a 0dBV, a pesar de que el nivel pro es más alto que el doméstico. Pero claro: falta considerar que el nivel pro son +4dBu y el consumo -10dBV, haciendo que se vuelvan las tornas.

El porqué de esa carga de 600 ohmios tiene que ver con cierto tipo de líneas que históricamente fueron importantes. El dBu se inventó para líneas telefónicas, de 600 ohmios y pequeña señal. Tenía sentido por tanto considerar como referencia 1mW y valorar qué nivel de tensión existía en esas condiciones. Ante cargas de 600 Ohm, el valor en dBu y en dBm coincide.

Pero como nivel para audio profesional no usamos los 0dBu, sino los +4dBu.

+4dBu son 1,23 V RMS o 1,74 V pico (senoidal)

De forma equivalente a lo que hemos comentado para el nivel audio doméstico, en el caso del estándar de nivel profesional:

• +4 dBu corresponden a una senoide de 1,23 V RMS y portanto una tensión 1,74 V pico

Y si queréis asociarlo a alguna idea de potencia, dicha tensión, en el caso senoidal, desarrolla una potencia de 2,51 mW pero sólo cuando la carga sea de 600 Ohm.

• +4 dBu corresponden a 2,51mW si la carga es 600 Ohm y la señal senoidal

Vuelvo a insistir en el interés que deberíamos tener por el valor pico, que es por lo que lo acompaño al más habitual valor RMS. Lo del valor RMS senoidal no nos importa tanto como el valor pico. Nuestras señales no van a ser senoidales, salvo al hacer algún test de equipos en plan laboratorio. Según el tipo de señal que manejemos podría llegar a haber picos muy destacados, por ejemplo en el habla o en una guitarra acústica con púa. Y lo que nos tiene que interesar es asegurar que no nos salimos del margen de funcionamiento correcto de los sistemas, cuyo límite viene asociado al pico.

Lo veremos con detalle en la siguiente entrega, ya os dije que hoy sólo queríamos definir estos niveles habituales en audio y la diferencia que los separa.

La diferencia de (casi) 12 dB entre -10dBV y +4dBu

No hay que confundir la diferencia entre esos dos niveles concretos, con la diferencia que separa una medida en dBV y en dBu.

Recordad que 0dBu correspondían a 0,775 V RMS senoidales (1,095 V pico) mientras 0dBV correspondía a una tensión más grande de 1V RMS senoidal y un nivel de pico de 1,4V aprox. Esa diferencia entre tensiones expresada en dB sería de 2,218dB. Como el dBu es una unidad algo más pequeña en valor que el dBV, el nivel de una determinada señal expresado en dBu tendrá un valor 2,21 dB más alto que expresado en dBV.

Cosa distinta es la distancia que separa los dos niveles diferentes de referencia-10dBV (un nivel bastante más bajo que 0dBV) y +4 dBu (algo más alto que los 0dBu). Concretamente, y recordando lo ya presentado:

• -10 dBV: 0,443 V (pico) o una senoide de 0,316 V (RMS)
• +4 dBu: 1,736 V (pico) o una senoide de 1,228 V (RMS)

Por lo que queda claro que +4dBu implica un nivel de voltaje casi unas 4 veces más fuerte que -10dBV. Y por tanto corresponderá a una potencia unas 16 veces más fuerte (una diferencia de aprox. 12 dB entre ambos niveles). Para ser más precisos 10 + 4 - 2,218 o lo que es lo mismo unos 11,782 dB más fuerte la señal ‘pro’ frente a la ‘consumo’. A efectos prácticos, unos 12 dB.

Lo podéis obtener también como resultado de esta representación gráfica:

La distancia entre los niveles de línea (-10dBV y +4dBu)

pablofcid

Una útil calculadora

Para los que hayáis tenido la paciencia de aguantar, viene un caramelo. Tenéis unacalculadora para convertir entre unos y otros valores, jugando con dBu, dBV, tensión pico y RMS, forma de onda, e cincluso con la impedancia, la potencia y los dBm, en la web de Analog Devices.

Las relaciones en voltaje hablan no tienen en cuenta el efecto de ‘carga’ o impedancia, mientras las relaciones en potencia sí. Así que la medida en dBm será coincidente con la medida en dBV o en dBu sólo en el caso de que la impedancia sea de 1000 o 600 Ohms, respectivamente. Y realmente pocas veces vamos a tener cargas de exactamente 1000 o 600 Ohm, así que la mayor parte de las veces la relación no es tan simple. Esa calculadora os ayudará a realizar este tipo de conversiones.

Artículo de Pablo F.Cid publicado en www.hispasonic.com

https://www.hispasonic.com/tutoriales/son-niveles-linea-10dbv-4dbu/43052

Latencia: el enemigo oculto en tus directos

Latencia es tiempo. Cuando debemos escuchar algo pero lo hacemos más tarde, tenemos latencia, así de simple. La latencia es un no tan nuevo pero desconocido, casi invisible y peligroso actor que se ha hecho protagonista con la inclusión de las tecnologías digitales. Nuestros compañeros del estudio de grabación dicen que lo conocen y bien, tratan de controlarlo de todas las maneras posibles: tienen tiempo. En realidad, invierten grandes cantidades de dinero en hardware específico que, justamente, abandera la baja latencia como claro elemento de juicio de compra, pero ¿qué pasa en el mundo del directo? ¿Es que no tenemos latencia? Claro que sí.

Existe latencia (o retardo) en toda conversión A/D y D/A: en toda. En los estudios el principal quebradero de cabeza es conseguir que si hay diferentes convertidores con latencias distintas, las señales lleguen exactamente en el mismo momento —difícil, pero no imposible—. Hay que elegir y, normalmente, supeditar los resultados a los límites que justamente la latencia impone (por ejemplo, utilizar diferentes previos analógicos pero un mismo convertidor A/D multicanal, retardarlo todo al valor más crítico o ajustarlo manualmente tras cada grabación). En directo este problema queda más o menos resuelto al utilizar exactamente el mismo convertidor en todos los canales de entrada y salida, por lo que la latencia será exactamente la misma para absolutamente todos los canales… en principio.

La latencia se suele medir en muestras (samples). Así, si sabemos que los convertidores de nuestro equipo presentan una latencia de 512 samples, podemos saber que, en el mejor de los casos, el retardo será de 0,023 s (multiplicamos por 2 esos 512 samples -entrada y salida- y dividimos el resultado por la frecuencia de muestreo que se utilice; por ejemplo, 44,1 kHz). 0,023 s o 23 ms ¿Son muchos o soportables? Depende.

Si realizamos una simple mezcla básica con ese dispositivo ya sabemos que lo que entre en la consola en analógico ‘saldrá’ 23 ms más tarde por su salida analógica. De ahí a un recinto acústico normal. 23 ms podríamos traducirlos como 9 metros, es decir, es como si comparándolo con una configuración analógica al 100 %, tuviéramos las cajas 9 metros por detrás. ¿Podemos mejorar esta latencia tan exagerada? Claro.

Los 512 samples que he utilizado en el ejemplo anterior suelen ser para ordenadores normales que se utilizan en un estudio de sonido. En realidad nuestra consola de audio para directo no es más que un ordenador pero específico para tareas de audio, por lo que las latencias de sus convertidores A/D y D/A son mucho menores. Como ejemplo, una simple medición nos permite comprobar que una Digico SD presenta sólo 0,09 ms de latencia entre SD Rack y local, mientras que en una CL5 la latencia alcanza unos nada menospreciables 1,98 ms en la propia consola (entrada/salida). ¿Problema resuelto? Claro que no.

Cada vez que entra en concurso un DSP o una parte de él, siempre, absolutamente siempre, se realizará con precisión la orden matemática a realizar, pero tal perfección tendrá como precio un nuevo retardo, una nueva latencia. Por ejemplo, en el caso de una Avid S3L-X, cada plugin que insertamos en cualquier canal añadirá, de facto, 2 samples de retardo por el simple hecho de ‘activar’ el rack de efectos, y 3 samples adicionales por cada uno de los slots utilizados. De hecho no son sólo 5 samples la latencia o retardo que se añadirá al canal, sino que cada plugin, en función de su cometido, tendrá un nuevo valor de latencia. Por ejemplo, el plugin Time Adjuster (aplica retardos de señal) añade 7 samples más. Eso quiere decir que si mi intención es retardar la señal 20 samples, en realidad tendré que ajustar el plugin para que sólo retarde 8 samples (8+7+2+3=20). Dichoso manual de usuario.

Pero, ¿qué ocurre si lo que quiero es hacer una compresión paralela de, por ejemplo, un bombo? Cojo el canal 1 que, procesado, lo envío a la salida máster, mientras que en el canal 2 añado el mismo bombo pero procesado diferente con el concurso de un plugin determinado. Como que es más complejo que el Time Adjuster anterior, su latencia es superior y, añadiendo los 5 samples que antes he mencionado, hacen que la señal una vez procesada me llegue al bus de salida máster 20 samples más tarde. Si la mesa trabaja a 48 kHz, esos 20 samples significan un retardo de 0,4 ms, es decir, 13,88 cm que podríamos traducir como la mitad de la longitud de onda de un tono de 1.250 Hz. ¿Lo véis? La suma de los dos canales provocará que, como mínimo, toda frecuencia de 1.250 Hz desaparezca. ¿Quién mezcla aquí: tú o la latencia? Teniendo en cuenta que tras el procesado ambas señales ya no son idénticas, los problemas que aparecen lo hacen en forma de phasing, atacando a más de una simple frecuencia.

Hay tres maneras de solucionar este problema. La primera es recurriendo a plugins que incorporen una opción de procesado paralelo, como el Pro Compressor de Avid. Tras ajustar la señal comprimida podemos sumarle al mismo tiempo la señal limpia y conseguir el mismo efecto de compresión paralela utilizando una combinación de señales coherentes en el tiempo. La segunda es utilizando la función de compensación de retardo (delay compensation), una prestación que no todas las mesas incorporan pero cuyo cometido es estar atentos a todos estos procesos que pueden provocar phasing y retardar (insisto: retardar) los canales correspondientes, pero sólo los canales correspondientes. A veces aceptaremos que el bombo y su compresión paralela (la suma de los dos canales) nos llegue 0,4 ms más tarde que la caja que no tiene compresión paralela (no dejan de ser sonidos diferentes), en vez de recurrir a la tercera opción: retardarlo todo, absolutamente todo, para que nos llegue tarde pero al mismo tiempo. Recordad que a esos 0,4 ms tendremos que sumarle los retardos correspondientes a las conversiones y otros procesados.

Esto es lo único que podríamos hacer, por ejemplo, con la Yamaha CL5. Recordemos que presenta una latencia media entre entrada y salida de 1,98 ms medidos en la misma mesa (no en un RIO, que alcanza retardos entre 3,06 y 4,06 ms según configuremos la red DANTE). El problema de esta consola es que no tiene compensación de retardo. Si nos sigue interesando insertar en el bombo en paralelo un compresor de su serie Portico tendremos un retardo añadido de 0,27 ms. Aunque es casi un 33% menos que en el caso de la S3L-X de Avid, lo único que tenemos es que el problema de phasing lo tendremos en una frecuencia más alta. Quizá no será un problema para un bombo al que no busquemos patada, pero imaginad una caja o, peor aún, las voces. Al no tener la posibilidad de poder mezclar ambas señales ni opción de Delay Compensation existe un truco muy viejo que es lo único que podemos hacer en este caso: utilizar un segundo slot e insertando el mismo plugin pero sin que actue y donde enviaremos todas las otras señales (o, como mínimo, el bombo que no tendrá compresión pero que deberemos mezclar con el comprimido). Puede parecer una buena noticia porque en realidad el tiempo perdido incluso es menor que en el ejemplo anterior, pero supone duplicar los recursos.

Las mediciones de latencia no son datos que habitualmente el fabricante ofrezca en sus especificaciones técnicas. Manteniéndonos en la CL5, cada vez que recurrimos a alguna de sus prestaciones añadimos más retardo a la señal (por ejemplo utilizar matrices o subgrupos). La inserción de un rack externo analógico sin duda alguna implica el concurso de dos convertidores digitales más (un primero D/A y un segundo A/D), lo que suma a nuestro canal unos vertiginosos 3,73 ms más de retardo. Si, además, lo que queremos insertar es algo como un Waves sin hardware específico, deberemos sumar la latencia de la conversión A/D y D/A de la tarjeta que utilicemos y, atención, todo el retardo de procesado que se añadirá en el rack virtual de Waves. Por algo será que Waves ofrece convertidores más rápidos y servidores específicos (más potentes y más rápidos). Aún sin el concurso de Waves, volvemos a lo de siempre: ¿son muchos esos 3,73 ms? Debes saberlo, calcularlo y empezar a entender el porqué a veces una mesa suena más “brillante” que otras: normalmente porque has realizado un procesado que, con esa mesa, no deberías realizar o, como mínimo, solucionar con antelación.

Pensemos, además, que esto mismo ocurre cuando después atacamos procesadores digitales: hay nuevos convertidores y nuevas latencias que van sumándose a nuestra cadena. Por eso empieza a ser relevante la interconexión digital que, aunque tampoco es la panacea, reduce no sólo los problemas de pérdida en las conversiones sino las latencias asociadas a conversiones D/A y A/D ya innecesarias.

Artículo de R.Sendra publicado en www.hispasonic.com

https://www.hispasonic.com/tutoriales/latencia-enemigo-oculto-tus-directos/43099

Margen dinámico: saturación y ruido de fondo en analógico y digital

Los niveles de entrada en saturación y de ruido de fondo son especificaciones esenciales de cualquier equipo. Tan esencial como es reflexionar sobre las profundas diferencias al respecto entre analógico y digital, de las que hablamos en este tutorial. Se trata de uno de los ejemplos más claros de las diferencias a la hora de enfocar el uso de sistemas audio digitales o analógicos. Diferencias que hay que conocer y saber atender para no flaquear o no aprovechar bien el potencial de cada uno de esos dos mundos. Porque a día de hoy es imposible desentenderse de ninguno de ambos.

Tras lo que reflexionemos y aprendamos en esta entrega, otra posterior profundizará en cómo optimizar la interconexión de sistemas audio, más allá de la simple concordancia de niveles 'nominales' (+4dBu o -10dBV también descritos en su propio tutorial).

Niveles y márgenes en analógico y digital, parecidos y diferencias

imagen tomada de freeimages.com

El rango útil de los sistemas

En cualquier sistema las señales que presentan sus entradas y salidas no pueden ser arbitrariamente grandes ni pequeñas en cuanto a su nivel. Hay unos umbrales o límites (superior e inferior) asociados a la zona de ‘normal’ funcionamiento.

Por la parte alta el límite está asociado a aquel nivel suficientemente elevado en la señal como para que se provoque distorsión. Por la parte inferior la cota la marcan todo un amplio juego de contribuciones no deseadas que contaminan a la señal a su paso por el sistema y que solemos resumir bajo el concepto de ‘ruido de fondo’ (aunque desde un punto de vista de rigor teórico no siempre correspondan al concepto estricto de un ruido). Esos son los límites de ‘normal’ funcionamiento en cuanto al nivel de las señales que condicionan un uso eficaz de los equipos y por tanto deben observarse en todo momento.

La distancia entre uno y otro nivel nos habla del máximo recorrido dinámico que podemos tolerar en las señales para que haya un tratamiento fidedigno de ellas en el sistema. Los detalles o momentos de nivel inferior al umbral bajo quedan enterrados en el ruido, los superiores al umbral alto quedan desfigurados por la distorsión.

El límite superior

El límite superior habla de que no se llegue a entrar en una zona de respuesta que entre en saturación y que dispare por tanto la distorsión. Como la saturación siempre se inicia por los ‘picos’ de la señal, que se achatan cuando el sistema ya no puede con más, el nivel ‘de pico’ (la tensión más alta de la señal) es lo que más nos interesa caracterizar para asegurarnos ese comportamiento ‘benigno’.

Es así especialmente en el caso de sistemas digitales porque en ellos una vez rebasado su fondo de escala se entra necesariamente en un recorte grave de la señal (el temido ‘clipping’) y es esencial garantizar que ningún pico rebase el fondo de escala previsto, aunque sea por un brevísimo lapso de tiempo. En digital hay ese máximo bien definido: el que corresponde al valor de la muestra más alta, que define la tensión ‘a fondo de escala’, y que de hecho a dado lugar a la definición de la medida dBFS (dB full-scale, o dB respecto a fondo de escala). De hecho, siendo exquisitos, conviene tener en cuenta que la señal de la que nos habla una representación digital puede contener algún valor ‘intermuestras’ más alto que ese fondo de escala (aunque eso es otra guerra que puedes revisar en nuestro tutorial sobre ‘true peak’).

En los sistemas analógicos la aparición de la distorsión es progresiva (codos saturantes suaves en los extremos de la zona de respuesta lineal de los circuitos) y puede ser más benigna y tolerable, pero en todo caso debe acotarse y eso implica también la necesidad de establecer alguna forma de límite superior al nivel.

Pico o RMS

Se trata por tanto de un codo ‘estricto’ en el caso digital y más ‘laxo’ en analógico,que da lugar a un tratamiento diferente.

Por eso, y aunque son siempre (tanto en analógico como en digital) los picos de la señal los que antes y más se distorsionan, sólo en digital es habitual pensar y medir en términos de pico (picómetro) y usar referencias ‘rígidas’. La referencia es el 'fondo de escala' y no deben sobrepasarse los 0dBFS (o mejor, los 0dBTP –true peak-). La preferencia por la medida 'pico' en digital surge de la absoluta necesidad de no superarlo para no caer en 'clipping'.

Sin embargo, el mundo analógico usa típicamente referencias de nivel RMS (root mean square) que ‘promedian’ el comportamiento de la señal durante un tiempo (pensad en el clásico vúmetro) y por tanto son medidas que no informan sobre los picos. Para compensar se dejan márgenes bastante amplios de confianza (‘headroom margin’) como holgura entre el nivel de referencia ‘0’ del vúmetro y la aparición de saturación significativa que se produce en realidad unos cuántos dBs más allá. El estandar sobre vúmetros exige que la marca 0 VU se alcance con una señal senoidal de 1kHz y nivel +4dBu. En la práctica muchos equipos no pro pueden incorporar medidores que no son propiamente 'VU-meters' sino realmente 'dB-meters', en tanto que su nivel '0' se corresponde con el que quiera que sea su nivel de referencia propio (por ejemplo los -10dBV). Pero quedémonos por comodidad con la denominación '0 VU' y sus +4dBu. El nivel ‘0 VU’ no es el nivel de entrada en saturación en estos sistemas analógicos. 0 VU no tiene un sentido equiparable a ningún ‘fondo de escala’ ni límite. Esa holgura y la presencia sólo ocasional de los picos permiten tener la confianza de que no habrá grave impacto sobre la señal, sabiendo además que aquellos picos que saturen lo harán de forma progresiva y no tan evidente ni dañina como el ‘clipping’.

No es extraño que un equipo +4dBu esté capacitado para operar sin entrar en distorsión severa con picos de hasta +24dBu, lo que implica que por encima del nivel 0 VU hay todavía una holgura de 20 dB. Esa amplísima holgura es la que permite que, pese a estar tomando referencias en RMS podamos estar algo más tranquilos sobre los picos. Recordad que 20dB son un factor 100 en potencia, y por tanto un factor 10 en amplitud: si mantenemos el vúmetro si rebasar los 0VU, los picos tendrían que ser 10 veces superiores a la tensión RMS para ser gravemente dañados. No imposible, pero sí poco frecuente.

Diferente naturaleza del límite superior analógico o digital

Esto evidencia ya unas diferencias significativas en el límite por arriba: la posibilidad de ser muy precisos en el terreno de lo digital pero acompañada de la gravedad de extralimitarse (menos mal que podemos evitar esa gravedad de consecuencias gracias a la fiabilidad y precisión tanto del objetivo como de las medidas), frente a una definición de límites mucho más borrosa en analógico y que puede valer pese a ser menos precisa por la ventaja de que su propio carácter ‘suave’ al saturar ayudará a disimular aquellos momentos en que algún pico se escape a pesar de las diferentes prevenciones adoptadas.

La forma de esquivar los problemas es completamente distinta: precisión, rigor y exigencia de observancia en lo digital, y un enfoque mucho más difuso e impreciso en lo analógico pero que finalmente funciona.

Aún así mi recomendación es en lo posible no basarnos sólo en medidas RMS y atender a también los niveles pico. No olvidemos que los vúmetros no cuentan toda la verdad que interesa. Aunque sólo fuera por ir sentando una cultura de 'cuidado con los picos' que es esencial en el uso de sistemas digitales. El colchón que da lo analógico es demasiado cómodo y veo preferible acostumbrarse a la mentalidad/rigor que exige lo digital cuanto antes. La magia analógica funciona, pero mejor ser conscientes de su presencia, para no quedarnos vendidos sin saber qué hacer cuando no esté presente.

El límite inferior

Una forma cómoda de cumplir el límite por arriba sería no intentar forzarlo, quedarnos cómodamente muchos dB por debajo, pero sabemos que no es tan simple porque no podemos olvidar que hay el otro límite, el inferior: el nivel de ruido de fondo, que actúa como un pedestal fijo por debajo del cual ya no tenemos una señal limpia sino principalmente ruido. Recorta por la parte inferior el margen dinámico del que disponemos. Así, todos los dB que queramos darnos de ‘colchón’ en la parte alta los sufriremos como pérdida de calidad mirando en la parte baja del recorrido dinámico, y por tanto hay que intentar trabajar en lo posible a los niveles máximos admisibles. Sólo así ampliamos todo lo posible la separación con ese ruido permanente que está ahí como indeseado pero inevitable compañero.

El ruido de fondo en analógico vendrá dado por la calidad de la electrónica empleada, pero no sólo por ella. También en buena medida por la complejidad del circuito, o para mejor decir, por la simplicidad del circuito: circuitos más simples implican menos componentes y por tanto menos ruido (cada componente añade su gotita al conjunto). No es extraño que muchos sistemas analógicos de alto nivel sean tan sencillos funcionalmente.

Salvo por contribuciones concretas como pueda ser un residuo del zumbido de red mal filtrado y que se cuele por la alimentación u otras vías, el ruido de fondo analógico es decarácter aleatorio y desvinculado de la propia señal. Algo que sólo podemos caracterizar de forma estadística, resumida en el nivel de ruido de fondo y quizá su color (si es ruido blanco, rosa, etc.). La presencia y nivel del ruido de fondo no dependen de la señal y están acompañando de forma persistente. Es una señal desconocida en su detalle pero bien precisada en su definición estadística, en su impacto, que además sucede igual sea cual sea la señal tratada.

Frente a esas características, en digital la limitación ‘por debajo’ está vinculada al llamado ‘ruido de cuantización’. Un valor estricto y bien conocido que se sitúa en los conocidos -96 dB para codificación con 16 bits o -144 dB para codificación con 24 bits en ambos casos referidos a lo que sería el nivel a fondo de escala. Pero no es tan simple: no es realmente un ruido.

16 y 24 bits y la ficción de los 96 y 144 dB

Al codificar con un determinado número de bits estamos transformando la señal, no añadiéndole ningún ruido (término que se reserva para cuando se trata de un añadido no relacionado con la propia señal). Como resultado esos valores teóricos de 96 y 144 exceden un poco de la realidad que percibimos. Es cierto que ese es el nivel de la señal diferencia entre las muestras sin cuantizar y tras la cuantización, pero como en realidad se trata de una distorsión (una versión ‘en escalera’ de la señal) y no de un puro ruido(un añadido no relacionado con el contenido de la señal) su percepción es muy diferente y llega a ser más notable que un ruido, al menos en momentos de poca intensidad de la señal. De hecho esa es la razón de ser del ‘dithering’: añadir a propósito ruido para disimular la presencia de esa distorsión, porque es perceptualmente más grato.

Así que, en cierta medida el aparente codo ‘rígido’ por abajo en la representación cuantizada (esos -96 o -144 dB) realmente es un poco menos estricto: dependiendo del tipo de señal, puede variar la ‘molestia’ sentida por culpa de la cuantización y ser algo más alto que lo que correspondería un ruido blanco de -96 o -144 dBFS. Sinceramente,24 bits hace ridículo plantearse estas finuras (más allá de 120dB de margen creo que tiene poco sentido hablar de ninguna cosa, ya todo es excelencia), pero con 16 bits sí es cierto que reduciría un poco esa demasiado alegre estimación de los ‘96’. Dejémoslo en que es una cota: será imposible sacar más de 96dB de margen, pero en la práctica hemos de pensar en que el margen útil es algo más reducido. El cuánto más depende de las características de la señal y por tanto no se puede definir a priori. Es un codo por tanto no tan definido como aparenta.

En 16 bit (no digamos ya en codificaciones de menor resolución) el resultado que apreciaremos con una mayoría de señales audio/habla/música será que para no maltratar los picos el nivel RMS quedará notablemente por debajo del 0dBFS y la sensación del ruido que tendremos será algo mayor de lo que prometían esos felices 96dB, para colmo siendo distorsión será más molesta que el puro ruido. Especialmente se notará en la medida en la que por fin se vaya apagando la guerra del volumen que ha llevado a sobrecomprimir todo tipo de músicas y vayamos recuperando el gusto por disfrutar un poco más de los detalles y contrastes.

Insisto: no son -96dB de ruido, lo son de distorsión. Pensad que si el nivel de la señal en un determinado pasaje es la cuarta parte del que correspondería al fondo de escala, estamos desaprovechando 2 bits y usando sólo 14, quedando temporalmente el nivel de esa distorsión de cuantización a -84dB respecto a los picos de la señal, lo que según el tipo de señal puede implicar tranquilamente unos -70 respecto a su valor RMS. Sumad que no es ruido sino una perceptualmente más impactante distorsión, y vais imaginando el panorama. No es grave, pero sí más limitado de lo que esperábamos.

Afortunadamente el uso de 24 bits, ya hoy muy estandarizado durante las etapas de grabación y producción, supone en la práctica que el ruido de cuantización casi siempre va a estar muy por debajo del ruido que van a tener ya presente las señales, porque incluso con electrónica de excelente calidad es bastante complicado obtener más allá de 120dB de ‘limpieza’ en analógico (y estoy siendo generoso, muchos sistemas audio no llegan a esa cifra). Desde ese punto de vista, y salvo que estemos grabando con niveles pico unos 20dB por debajo del fondo de escala, codificar con 24 bits en la práctica no va a introducir más ruido del que ya traen las señales. Es decir, no las van a empobrecer, la cuantización no las va a degradar en ninguna forma apreciable.

En el paso final a formatos de 16 bits sí que se necesita un mimo especial para acercarnos a la cota de los 96 dB, casi siempre vigilando y recortando picos con algún tipo de compresión/limitación, y tal vez haciendo uso de 'dithering', lo que se decidirá en función de los resultados y escuchando si es preferible un ligero incremento de ruido frente a la escucha de la distorsión a bajos niveles.

Diferencias en el límite inferior analógico o digital

Hablando de los momentos débiles de la señal nos encontramos por tanto con una situación en parte invertida respecto a la que planteábamos con el límite superior.

Es el límite inferior analógico el que sí nos ofrece una referencia ‘fija’ aunque probabilística (su nivel de ruido de fondo) y que es realmente independiente de la señal. Mientras, el mundo digital cuenta con un límite que tiene una valoración global fácil (los 96 o 144 dB) pero cuyo impacto real es variable. Dependerá de la señal por tratarse realmente de una distorsión, y será mayor cuando mayor sea el valor de cresta (diferencia entre valor pico y valor RMS) tenga la señal. Pero compensando esta cuestión de la sensibilidad a la señal en las sensaciones que por la parte baja del margen dinámico ofrece lo digital, está el hecho de que si bien puede llegar ser apreciable en 16bit, en 24 será mucho menos importante dado que dominarán típicamente los cuellos de botella que ya estén imponiendo otras partes analógicas del sistema.

De la filosofía a la práctica

Sacaremos provecho a este debate de hoy en una entrega posterior enfocada a ofrecer reflexiones, consejos e información sobre cómo conectar equipos audio de forma óptima. Algo que como veremos allí, no se resuelve sólo atendiendo a la etiqueta +4dBu o -10dBV que acompañe a entradas y salidas, hay más cosas que tener en cuenta.

Artículo de Pablo F.Cid publicado en www.hispasonic.com

https://www.hispasonic.com/tutoriales/margen-dinamico-saturacion-ruido-fondo-analogico-digital/43058