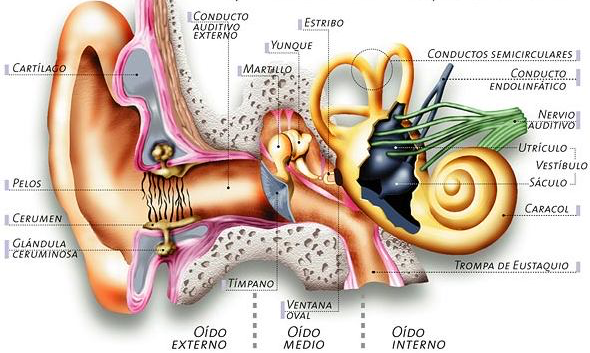
El sonido como onda, nuestra etérea materia de trabajo
El sonido para nosotros, interesados por no tanto por su aspecto estrictamente acústico sino por su vertiente de comunicación y artística, nos lleva en última instancia a preocuparnos más por su percepción y por las sensaciones que estimula en un oyenteen nuestro caso humano que por su estricta definición desde la física. De igual forma la electrónica (entendida en un sentido amplio capaz de englobar desde la electroacústica, a la electrónica analógica o también lo digital y los sistemas basados en ordenador, pese a las enormes diferencias) no nos interesa tanto en su esencia interna y sus circuitos sino en sus aspectos ‘sistémicos’ y su acción sobre las señales que tratamos en esa forma ‘electrónica’. Es decir, una visión ‘desde fuera’ y centrada en su uso y sus prestaciones, más que en la especificación y entendimiento detallado de su diseño, que corresponderían a la ingeniería.
Pese a ello, para una actividad profesional, eficaz y eficiente, no podemos escudarnos en el ‘todo vale por el arte’ para desatender un mínimo de conocimientos vinculados a acústica y electrónica. Ese conocimiento de base será el que nos permita desarrollar una actividad sostenida en el tiempo: capaz de lidiar con las constantes evoluciones de las técnicas y sistemas, y capaz también de adaptarse a muy diferentes entornos de trabajo y muy diferentes requisitos de clientes.
Es cierto que, al final, “si suena bien, está bien”. Pero llegar a que suene bien no como producto de la casualidad sino de un trabajo conocedor de la relación entre los medios y los resultados es lo que nos hará tener un papel que jugar en el mercado, una constancia en nuestro nivel de calidad, y una eficiencia que nos permita ajustar los tiempos y costes de nuestra labor en un rango sensato. Labor artística es por ejemplo la de los músicos, pero la nuestra, hay que asumirlo, es una labor mucho menos artística y creativa, mucho más objetivable y ajena al ‘todo vale’, aunque tenga sus momentos de sensación y a veces realidad creativa.
Evitaremos casi siempre la visión del diseñador y sus complejidades físico-matemáticas, pero insistiremos en entender las causas y efectos cada una de las parcelas de lo acústico y lo electrónico que iremos desgranando. No nos importará desconocer cómo se diseña un reflector acústico, pero sí deberemos entender lo básico de su funcionamiento y el significado de sus especificaciones. No nos preocupará cómo se crean los planos de un auditorio para conciertos, pero sí qué es lo que puede llegar a suceder dentro de él. Las tripas de un amplificador nos importarán menos que la forma en la que podemos escuchar, conocer y aprovechar las diferentes características que puede presentar. Y así podríamos continuar.
Nuestra ¿materia? es el sonido
En las primeras entregas vamos a tratar sobre la materia con la que trabajamos: el sonido. Una materialidad singular, por cuanto más que entenderlo como ‘objeto’ el sonido lo entendemos como ‘onda’, como fenómeno que sólo se entiende ‘en movimiento’ y que es capaz de propagar una señal.
El sonido de un timbal no es ni la vibración de su parche ni la vibración del tímpano, menos aún es nuestra sensación al percibirlo o el efecto que desencadena en nuestro cerebro o la reacción que nos provoca. Pese a que el parche, el tímpano y el cerebro sean necesarios para que escuchemos ese timbal, por el sonido del timbal nos referimos a la propagación, a través normalmente del aire, que permite que una parte de la energía que emana del mismo llegue a nuestro tímpano y nos provoque una sensación. El sonido son esas vibraciones en viaje a través el aire.
Cuando hablamos de señal sonora hacemos referencia las más de las veces no a la onda sonora en sí, sino a su representación en todo tipo de formatos. A través de una combinación de sistemas artificiales acústicos, electrónicos e informáticos (incluso a veces ópticos), somos capaces de registrar/manipular/reproducir el sonido. Recogiendo su ‘forma’ en el aire con micrófonos queda convertida en una señal, inicialmente eléctrica, que podemos registrar en todo tipo de formatos, sean analógicos o digitales, y basados en vinilo, cinta, discos ópticos, memorias digitales… Esas representaciones del sonido pueden con facilidad someterse a tratamientos diversos, gracias a la versatilidad de la electrónica y no digamos ya de las técnicas de procesamiento digital por vía de hardware específico o de software para ordenadores de propósito general. Volver esas señales a sonido viajante en el aire con una potencia adecuada es cometido de los amplificadores y altavoces.
Pero todo el abanico enorme de posibilidades tecnológicas sobre las señales sonoras no debe hacer que olvidemos empezar con lo que es principio y fin: el sonido en sí y sus representaciones como señal.
No está de más recordar qué es lo que caracteriza una onda y entender con ejemplos sencillos que no olvidemos jamás algunas características, que si se abordan sólo desde las matemáticas muchos no llegan a comprender de forma suficiente.
Fenómenos ondulatorios
Los fenómenos ondulatorios son bien conocidos por todos porque en la escuela obligatoria se nos presentan y también porque tenemos presencia de ellos en la vida ordinaria. Hablar de una onda es hablar de la posibilidad de transmitir energía de un punto a otro sin desplazar materia.
Algo que entendemos mejor con el clásico experimento consistente en suspender varias bolas alineadas y desplazar la primera soltándola para que impacte en la siguiente. Acaba haciendo que la última bola sea impulsada. Si la hilera fuera infinita la propagación de ese impacto no cesaría, avanzaría permanentemente de bola en bola. Eso es en esencia lo que implica el concepto de onda: la capacidad de desplazar no un objeto (una partícula concreta), sino una energía o una acción (un movimiento en este caso).
Al final del experimento las bolas individuales siguen en su sitio, pero hemos conseguido que el impulso inicial se vaya propagando sucesivamente por bolas cada vez más alejadas y que sea la última de ellas la que salte proyectada, al no tener otra que la frene. Esa es la idea de una onda o fenómeno ondulatorio: la capacidad de propagar la perturbación sin necesidad de que ‘globalmente’ nadie se mueva de su sitio. Consigo que mi impacto, realizado sobre la primera bola, acabe siendo ‘virtualmente’ aplicado a la última. Finalmente no viaja ninguna bola, viaja el impacto.
Se ha generado una propagación del impulso inicial. Una propagación que se desarrolla a lo largo del tiempo (no es instantánea, lleva su tiempo) y del espacio (se va moviendo de lugar hasta llegar a apreciarse en la última). Por tanto tiene, como no podía ser de otra forma, una determinada velocidad de propagación.
Dejando de lado los debates de física profunda sobre que todo en el universo es onda y partícula a la vez, desde nuestra visión macroscópica apreciamos con más facilidad los fenómenos ondulatorios allí donde hay varias partículas fáciles de identificar, como las bolas del ejemplo.
Pero esto mismo sucede en el caso del sonido: cualquier vibración originalmente mecánica en un objeto (algún tipo de desplazamiento) acaba afectando al aire próximo a ese objeto. Como resultado una parte de la energía de esa vibración pasa al aire, iniciando una acción ondulatoria soportada por las partículas (moléculas) que forman el aire y que alcanza a lo largo del tiempo posiciones cada vez más alejadas. Puede que no las veamos, pero esas moléculas del aire están ahí, como las bolas, ejerciendo de imprescindibles elementos ‘conductores’ para la propagación de la onda (no hay onda ni por tanto sonido en el estricto vacío, al carecer de un medio soporte para el viaje de la onda).
Ondas longitudinales/transversales y en línea/planas/esféricas
El de las bolas era un ejemplo de onda que desarrolla su viaje ‘en línea’, porque así lo era el medio que le servía de soporte para el viaje. Además era una propagación longitudinal: el movimiento individual de las partículas (las bolas de la cadena) se produce en la misma dirección por la que avanza la onda.
También es una onda ‘en línea’, pero en este nuevo caso transversal, la que se original sobre una cuerda cuando la percutimos. El desplazamiento que infringimos en un punto concreto de la cuerda es ‘arriba/abajo’, pero la propagación de ese impulso inicial se desarrolla hacia ambos lados hasta extenderse por toda la cuerda. Con una cuerda infinitamente larga, se trataría de un movimiento de ‘fuga’ permanente hacia los extremos. En la cuerda del piano, el movimiento acaba siendo periódico porque la cuerda es finita y está anclada en ambos extremos, con lo que al llegar a ellos ‘vuelve’ hacia atrás, y se acaba generando un patrón repetitivo, cuyo ciclo o periodo depende de la longitud de la cuerda (y de su material, tensión, etc.).
Los ejemplos anteriores han mostrado ondas que avanzan ‘en línea’, al estar confinadas a un medio de propagación que es lineal.
Hay también ondas que se desarrollan no en línea sino en una superficie. Al lanzar una piedra al centro de un enorme estanque, vemos la formación de una onda que se propaga por toda su superficie como una perturbación en forma de circunferencia cada vez más extensa pero de menor altura (hay que repartir la misma energía en un espacio cada vez mayor). Tenemos aquí una propagación de la onda que observamos en dos dimensiones, es decir, en un plano (ya no en línea). Y aparece con claridad el concepto del reparto de la energía: al extenderse a un ámbito mayor la onda, el movimiento pierde vigor, pierde nivel. Cuanto más lejos estamos de su ‘epicentro’ más pequeña es la amplitud de la perturbación que se observa. Algo que no sucedía en la línea de bolas, que siendo lineal no amplía el ámbito (al menos en las condiciones ideales en las que nos movíamos hasta ahora: hemos despreciado en todo momento las pérdidas por ‘fricción’ y otras que en un caso real serían una causa adicional de reducción del nivel con la distancia).
Igual que puede haber propagación en dos puede darse en tres dimensiones, y así podemos verlo en el caso del sonido: un chasquido de los dedos dará lugar a que se propague un sonido en forma esférica alrededor de ese punto desde donde se produjo el chasquido (suponiendo que no hay obstáculos, ni siquiera el de la persona dueña de los dedos) y cada vez con un radio mayor. Y como la superficie de la esfera depende del cuadrado del radio, la reducción de la potencia será cuadrática. La propagación del sonido en el aire es de tipo ‘longitudinal’ (las partículas del medio realizan su movimiento en la misma dirección en que avanza la onda) y en ausencia de obstáculos es 'esférica' (salvo cuando confinamos el sonido en un espacio o conducto que condiciona su libre avance).
El sonido como onda
Pensad en la entrada en vibración del parche de un timbal cuando en realidad sólo hemos alimentado un impulso mediante un golpe único con una baqueta. El movimiento del parche desplaza el aire que está inmediato a su superficie, y así parte de la energía aportada al timbal acaba siendo comunicada al aire que lo rodea iniciándose una onda sonora en el aire.
Pensemos de momento no en el movimiento ‘sube/baja’ repetitivo del parche tras un único impacto, sino sólo en su primer recorrido. En un único desplazamiento en el que una cara del parche ‘aprieta’ el aire que está de un lado, mientras la otra cara crea un ‘vacío’ o ‘succión’ que el aire se apresta a rellenar. Olvidemos también que aquí el objeto vibrante no es ‘puntual’ (algo que aproximadamente podíamos pensar en el chasquido de dedos), sino que tiene unas determinadas dimensiones.
Las moléculas empujadas (que dan lugar a una concentración mayor de partículas) chocarán con las siguientes en su camino, impulsándolas a moverse y por lo tanto la ‘concentración’ irá trasladándose por el espacio. Las moléculas ‘succionadas’ (que dan lugar a una concentración menor) crean una escasez de partículas que obliga a otras cercanas a desplazarse para reequilibrar, y ese desplazamiento origina el movimiento virtual de esa escasez de partículas. Al final tenemos la concentración y rarefacción desplazándose por el medio aire. Tenemos la onda sonora.
Las moléculas del aire no están quietas nunca (el aire es un fluido), están en permanente movimiento, tanto más agitado cuanta mayor sea la temperatura. Pero por defecto la ‘densidad’ de las moléculas es homogénea. Están repartidas por igual en todo el espacio. La acción del parche en movimiento desplaza las moléculas más cercanas. Y el empuje o succión que ejerce el parche sobre las moléculas cercanas acaba provocando cambios en la densidad en ese entorno. El aire estará más comprimido o más relajado de lo que debería. Esto desencadena una propagación como consecuencia de la tendencia a recuperar la situación original de ‘equilibrio’ en cualquier fluido. En ausencia de obstáculos, esas compresiones y rarefacciones del aire se propagan en el espacio alcanzando a lo largo del tiempo cada vez posiciones más alejadas.
Velocidad del sonido y sus consecuencias
La velocidad con la que se propaga la onda sonora en el aire (en el vacío no habría propagación) depende de factores como la temperatura, pero una referencia típica lleva a hablar de unos
aprox. 340 m/s (a temperatura ambiente rondando los 25ºC)
Es relativamente veloz, pero sin exageraciones: unos 1250 km/h. Todos tenemos la experiencia de ver el relámpago mucho antes de oír el trueno porque la velocidad de la luz es mucho más alta que la del sonido.
Esta velocidad de unos 340m/s, combinada con el rango de frecuencias en que sucede la audición humana (que solemos considerar, algo generosamente, que abarca de 20 Hz a 20kHz) implica consecuencias importantes.
Al cabo de un segundo de estar produciendo una determinada señal, esta se habrá propagado por 340 metros que estarán ya ‘ocupados’ con señal. Si la señal es de 20Hz, en ese mismo segundo se han generado en la fuente 20 ciclos. Esos 20 ciclos están ocupando esos 340 metros, y por tanto cada ciclo individual de una señal de 20 Hz está ocupando en el aire 340/20 = 17 metros. La duración temporal de un ciclo de 20 Hz es 1/20 = 0,05 segundos. Es decir, un ciclo de 20Hz dura 50 milisegundos.
Si la señal es de 20kHz, un razonamiento idéntico nos lleva a que cada ciclo individual de una señal de 20 kHz está ocupando en el aire 340/20000 = 0,017 m = 1,7 centímetros, siendo su duración de 50 µs (microsegundos).
Para un sistema de grabación/procesamiento/reproducción de audio esta enorme disparidad de ‘tamaños’ y condiciones de señal implica unas complicaciones de diseño importantes. Sobre esta cuestión podéis revisar este tutorial específico. Nuestras señales audio se extienden por nada menos que 10 octavas de espectro audible, dentro del que es habitual la presencia de numerosos armónicos (concepto al que dedicaremos atención y que en otras señales muchos más limitadas en banda no llega a existir). Los transductores (micrófonos y altavoces, por ejemplo) deben ser capaces de atender esa dispersión de tamaños (por eso la presencia de altavoces multivía, por ejemplo). Podríamos seguir acumulando más casos ilustrativos que muestran condiciones difíciles sin duda.
Pero quiero que entendamos desde ya la especial característica del extremo de los 20Hz.
Los 20 Hz y los 20 kHz, dos extremos muy diferentes
En el extremo agudo, y bastante antes de los 20kHz, muchas personas no tendrán ninguna sensación auditiva. Además el desvanecimiento de esa sensación es progresivo, no es estricto. Nos cuesta bastante escuchar una señal de 15kHz, y aún más percibir una de 18kHz. Tenemos una disminución gradual de la capacidad de audición cuando ya nos estamos acercando al extremo alto, llegando un momento en el no percibimos ningún sonido. En ese extremo alto vamos ‘dejando de oír’ a medida que subimos en frecuencia.
Pero pensando en señales que oscilan con ciclo de 20 Hz no se elimina la audición sino que cambia cómo se percibe la señal.
Las señales de frecuencia superior a unos 20 Hz se oyen como un ‘continuo’, mientras para señales de frecuencia inferior a esos 20 Hz lo que percibimos son los ciclos individuales, cada ciclo provoca la sensación de escucha aislada de un evento sonoro. Así sucede con las señales más habituales, que son complejas y no simples senoides sino otras formas de onda (una senoide pura de frecuencia tan grave se siente más 'corporalmente' que por audición). Si tuvierais un martillo mecánico podríais comprobar que si percutís una mesa digamos diez veces por segundo oís los golpes individuales, tenemos capacidad de reconocerlos y aislarlos unos de otros. Hay una sensación de escucha de los 'impactos’ uno a uno. Lo podéis hacer también golpeando con el dedo una superficie o con un sintetizador y un equipo decente de audio, llevándolo al registro subsónico y usando por ejemplo onda en rampa o cuadrada.
Cuando seguimos subiendo la frecuencia del martillo o del oscilador del sintetizador (el dedo ya no llega a ser suficientemente rápido) hay un momento en que la escucha de los eventos aislados se complica, parecen fundirse tanto que se dificulta la escucha individual y escuchamos un burbujeo de impulsos en el que notamos que hay cierta variación, que tiene algún tipo de estructura temporal, pero en el que somos incapaces de contar o percibir los golpes uno a uno. Y un poco más allá ese burbujeo inestable da paso a una sensación de escuchar un tono, un sonido afinado y estable, que percibimos como una señal mantenido en el tiempo, sin incidentes ni impulsos internos. El martillo electrónico, puesto a percutir, digamos a 25 o 30 veces por segundo, y más claramente aún a 40, no nos dará sensación de martillo que golpea varias veces, sino de un sonido constante no muy diferente (salvo por su timbre) del que esperamos encontrar en un instrumento musical cuando produce una nota.
Es por tanto especialmente relevante este límite de los 20Hz o equivalentemente de los 50ms de duración de ciclo (siempre un valor aproximado y dependiente de cada persona y cada situación), porque marcará unas diferencias en los procesos de interpretación de lo oído muy relevantes. Y es un límite que no sólo se refiere a la escucha de señales cíclicas, también actúa en otras muchas cuestiones vinculadas a la audición.
Por ejemplo en la cuestión de los ecos. Siendo 50ms la distancia temporal que han de guardar dos objetos sonoros semejantes para que no sean confundidos en uno, la presencia de un rebote de la señal audio en una pared generará sensaciones muy diferentes según alcance al oyente antes o después de ese tiempo.
Los rebotes en paredes a gran distancia (como se llegan a producir en un frontón, o aún más en las montañas) nos permiten percibir el ‘eco’, oyendo como disjunta la repetición respecto al sonido inicial. Sin embargo en salas más pequeñas (recordad que los 50 ms y los 20Hz implican 17 metros en el aire) los rebotes van a llegar tan cercanos que la incapacidad del oído para separar el original y su repetición entra en juego. Lo que tenemos es una sensación de escuchar una sola vez pero con un sonido que está ‘afectado’, cambiado. La presencia del rebote combinado con el sonido original realza algunas frecuencias y rebaja otras, en un efecto resultante conocido como ‘filtro peine’ (comb filter) que tenéis revisado en este tutorial.
Otra situación típica en la que se percibe ese cambio de la forma de percibir a partir de los 20Hz hacia abajo (o equivalentemente de los 50ms hacia arriba), sucede con, por ejemplo, las modulaciones tales como el vibrato o el trémolo. Un vibrato (variación cíclica de la altura/tono de una nota/sonido) musicalmente útil suele ser de pocos Hz. En los sintetizadores y por medios artificiales podemos generar vibratos más veloces. Pero cuando la velocidad de la vibración la llevamos por encima de aprox. 20 Hz ya no oímos un vibrato. Oímos primero una nota que parece sencillamente inestable, algo ‘mareada’ y desubicada. Y si seguimos subiendo llega un momento en el que oímos un cambio de timbre, una nueva nota con un tipo de sonido diferente, y que varía mucho con la frecuencia a la que se realiza el vibrato y con su intensidad. Tanto es así, que es ese el concepto que subyace en una técnica de síntesis conocida como síntesis FM (síntesis por modulación en frecuencia), de la que podéis conocer más en varios capítulos de nuestrocurso de síntesis.
La alternancia del sonido (bipolaridad, AC vs DC)
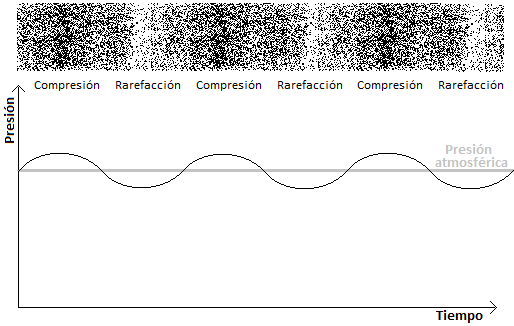
En el aire existe una presión atmosférica fija que no llega a producir ninguna sensación sonora. Su valor es diferente según estemos a nivel del mar o en una montaña, entre otras cuestiones. Pero tratándose de un valor esencialmente fijo (al menos en cada momento y lugar) el oído no se ha desarrollado para ‘medirlo’, sencillamente no hace caso de ese valor medio. Es necesaria la variación en torno a ese valor medioconstante para tener sensaciones auditivas. El sonido es por tanto una señal ‘bipolar’, que oscila por encima y por debajo de un nivel de referencia que arbitrariamente consideramos nuestro nivel cero. Así, la señal sonora será una de constante cambio por encima y por debajo de ese nivel de reposo o nivel 0. Son los cambios los que aportan información sonora, y no el nivel de referencia.
Es por esto que muchos sistemas audio sólo registran o procesan la componente alterna (AC) y bloquean cualquier componente continua (DC). Muchas veces decimos que el sonido carece de continua. Más que hablar de ‘ausencia’ de continua debemos hablar de‘irrelevancia’ de cualquier componente continua. Sólo nos interesa la componente alterna.
Sonido como compresión y rarefacción del aire en torno al valor de la presión atmosférica
pablofcid
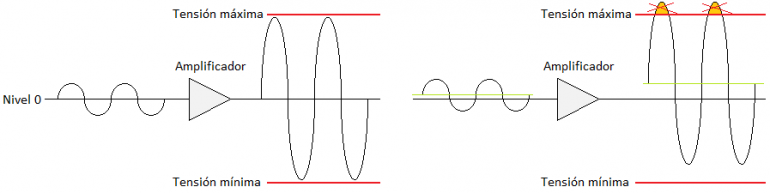
Muchos de los sistemas audio trabajan mejor sin presencia de DC y por ello la eliminan. La razón se entiende con facilidad pensando en el caso, típico, de un amplificador que admite en su salida unos determinados niveles de tensión máxima y mínima. Si la señal audio entra sin DC la excursión de la señal en la salida puede llegar a aprovechar bien todo el recorrido disponible. La presencia de DC en la entrada dará lugar a una componente DC amplificada en la salida que llevará con facilidad a menor aprovechamiento del margen útil del amplificador porque uno de los extremos llegará a la saturación mientras el otro está aún lejos de su frontera.
Porqué evitamos la DC en los sistemas audio
pablofcid
Pensad también que la presencia de DC en la señal entregada a un altavoz hace que esté circulando por él una corriente continua, que mantendrá el cono desplazado respecto a su posición de reposo ordinaria (con lo que también haremos que sature antes). Son ejemplos de entre muchas situaciones que muestran lo inconveniente de la presencia de DC en las señales.
Es habitual por ello el uso de ‘condensadores de desacoplo DC’ en las etapas de entrada / salida, que bloquean cualquier continua y no la dejan pasar a nuestros sistemas audio. Pero no pocas veces esta retirada no se limita sólo a la pura DC sino que afecta en alguna medida a las componentes más graves. Al fin y al cabo los 20Hz no están tan alejados de la pura DC. Por eso mismo existen también sistemas audio que proclaman como bondad el llegar a poder tratar señales DC. Sucede por ejemplo con muchos interfaces de conversión A/D y D/A. La importancia del registro bajo y sobre todo de lo infrasónico (como generador de sensaciones físicas en cine, audiovisual, y música electrónica ‘de baile’, p.ej.) ha traído consigo esta necesidad de extender el ámbito grave de los sistemas.
Pero el diseño de estos sistemas tolerantes a DC es más costoso y permanecen muchos que no lo son. Y a la postre, el estricto ‘DC’ no es realmente algo que nos interese como señal sonora y casi siempre convendrá eliminar, aunque nos beneficiemos del extenso recorrido infrasónico de algunos sistemas.
La representación de las señales sonoras será por tanto casi siempre ‘centrada en cero’, haciendo obviedad de cualquier componente DC, retirándola en caso necesario.
En audio solemos trabajar con señales centradas en 0
pablofcid
Entendiendo el sonido como esas variaciones de presión que se propagan por el aire, puede quedar representado como una señal que varía a lo largo del tiempo que podemos llamar s(t) (una función que describe la señal o sonido a lo largo del tiempo), y en la que, como hemos dicho, hacemos abstracción de su posible nivel de continua para quedarnos sólo con los cambios.
Podemos capturar con un micrófono esa señal y crear con ella una gráfica de su desarrollo a lo lardo de un eje horizontal de tiempo.
Representación temporal (forma de onda)
pablofcid
s(t) describe en el fondo una ‘amplitud’ o nivel instantáneo de la señal sonora. Podrán ser voltios (más bien microvoltios) en la salida del micrófono, niveles de campo sobre la cinta magnetofónica, o micras de desplazamiento en el microsurco del vinilo.
En las representaciones analógicas es habitual esta presencia de una determinada unidad que da un significado físico concreto a la amplitud de la señal. Pero también podremos concebir una s(t) sin unidades en el caso de que queramos hacer abstracción de ellas y queramos concentrarnos sólo en la forma y nivel ‘relativo’ de la señal, sin referencias a algún tipo de unidad absoluto. Es lo que sucede de forma consustancial a la digitalización.
La representación digital: fondo de escala y su carácter adimensional
Aunque tendremos que abordar con mucho mayor detalle la cuestión de la digitalización más adelante, es bueno que contrastemos ya esas definiciones de amplitud vinculadas a una unidad física, tan habituales en los dominios analógicos, con lo que obtenemos tras la digitalización: una ristra de valores que representa la amplitud de la señal en instantes concretos mediante una codificación numérica de su valor con una determinada profundidad de bits. Una doble discretización del tiempo y del valor que permite concebiren la versión digital una señal s[n] adimensional que representa sólo ‘forma’ de la señal en una ristra de números.
Discretización del tiempo: En la señal digitalizada s[n] el tiempo sólo avanza en saltos discretos. A la velocidad definida por la frecuencia de muestreo capturamos el valor instantáneo de la señal. El hecho de usar ‘n’ (y no ‘t’) pretende evidenciar el carácter discreto en el tiempo, dado que n sería un número entero con el que representar el avance por sucesivas muestras (la muestra 0, 1, 2, 3…). Bajo determinadas condiciones (básicamente que la señal de partida esté limitada en banda a la mitad de la frecuencia de muestreo) se demuestra la posibilidad teórica de una reconstrucción perfecta, que a día de hoy se logra también en muy buena medida pese a los condicionantes prácticos de los sistemas (ya abundaremos en ello en otro momento).
Discretización del valor (de la amplitud): La amplitud encontrada en cada uno de esos instantes de muestreo, no se guarda con infinita precisión. En la señal digital la amplitud no es cualquier valor, está también discretizada. Con 16 bits tenemos 216 combinaciones de unos y ceros posibles, que implican 216 = 65536 valores de amplitud posibles. Con esos 65536 valores cubrimos el rango de trabajo del conversor, usando saltos de idéntica magnitud (en el caso habitual de que usemos codificación ‘lineal’ -linear PCM-, tiempo atrás, con sistemas de 8 y 12 bits era habitual una codificación no lineal que una mayor cantidad de bits hace innecesaria). Con 24 bits tenemos 224 = 16777216 y por tanto una representación aún más precisa del valor instantáneo, que ya resulta en la práctica indistinguible del valor continuo original, porque el ruido que acompaña siempre a las señales reales es de magnitud mayor que la que separa dos valores consecutivos de nuestra escala discreta (es mayor el error o incertidumbre causado por el ruido que por la digitalización con 24 bits).
El carácter ‘adimensional’ de la señal digitalizada
En todo caso el valor de cada muestra está codificado con una determinada cantidad de bits y hay un límite máximo y mínimo del recorrido que el conversor admite. Valores extremos que solemos escribir (porque es sencillo) como +1 y -1 para representar esas cotas máximas que, una vez estamos en la representación digital, nos importa poco sean referidas a una determinada cantidad de voltios o cualquier otra unidad. Son sólo referencias del máximo y mínimo valor que tienen cabida dentro del rango de trabajo del conversor. Podríamos llamarlos igualmente 100% y -100%, o cualquier otro rango que nos apeteciera indicar.
Los valores guardados en un fichero audio como representación de la señal sonora no indican cuántos ‘voltios’ habrá que producir para volverla a generar, sólo la ‘forma’ de la señal a lo largo del tiempo, valores relativos a un máximo que cada conversor D/A podrá situar a su propia voluntad. En cada conversor un mismo fichero podrá ser reproducido a uno u otro nivel, según cómo esté resuelta su etapa de salida.
Surge así el concepto de ‘valor a fondo de escala’. El valor máximo (y el mínimo) en la representación de un fichero de audio digital no indican en sí ningún valor concreto, sólo indican qué porción del recorrido máximo representa cada muestra. Es entre las especificaciones de los conversores donde encontraremos cuál es el valor de tensión (voltios) que cada D/A produce en su salida cuando recibe la combinación de bits correspondiente a alguno de los dos extremos de la representación digital.
Artículo publicado por Pablo Fernández-Cid en www.hispasonic.com
https://www.hispasonic.com/tutoriales/sonido-como-onda-nuestra-eterea-materia-trabajo/43285